Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.3. Термодинамические константы диссоциации протонированных моно- и диоснований
Рассмотрим процессы взаимодействия основания (В) с сильной полностью диссоциированной кислотой (титрантом):
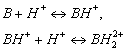(5.4)
Термодинамические константы диссоциации протонированного основания (Ка) после преобразования уравнения (5.1) могут быть представлены следующими соотношениями:
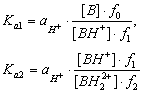(5.4)
В уравнении (5.4) 
- активность ионов лиония, то есть сольватированного иона водорода, в последующем примем обозначение а(SH+), в любой точке потенциометрического титрования; 
- равновесные концентрации нейтрального и протонированного многокислотного основания в процессе титрования сильной кислотой; 
- коэффициенты активности нейтральной и протонированных форм полиоснования.
Как отмечалось ранее [31], известные методы оценок ионной силы при кислотно-основном равновесии [24, 25, 29] основаны на использовании концентрации первой ионизированной частицы, например, [ВH+] для двухкислотного основания. Было показано [7, 40], что в расчетах констант диссоциации не следует пренебрегать равновесными концентрациями остальных ионов, так как их величины в различных точках титрования сопоставимы с концентрацией первого протонированного иона, значительно влияют на значение ионной силы раствора и, как следствие, на величину термодинамических констант кислотной диссоциации поликислот и протонированных оснований. Наиболее приемлемым и оптимальным способом оценки ионной силы, определяемой с учетом равновесных концентраций всех заряженных частиц, является представление кривой титрования основания в логарифмических координатах. При этом равновесные концентрации всех частиц, образующихся при титровании диоснования: 
, могут быть определены на диаграммах -lg а(SH+) – lgC [7, 40]. Оценка значения коэффициентов активности f0, f1, f2 проводится по более приемлемому методу Дэвиса [9] (уравнение 4.5)
(4.5)
где I – ионная сила раствора, определяемая по известному уравнению: 
).
Протонированные диоснования характеризуются близостью констант диссоциации, поэтому определение значений последовательных констант диссоциации в водных растворах, тем более в среде органических растворителей, весьма затруднено из-за совместной нейтрализации функциональных групп.
Разработку теоретической и экспериментальной модели расчетов термодинамических констант диссоциации протонированных форм и нейтральной молекулы основания в среде органического растворителя покажем на примере титрования основания (например, аминов) сильной кислотой (пикриновой кислотой). Для этого необходимо предварительно определить стандартный потенциал цепи (II).
Cтеклянный электрод / НСlО4 / AgCl, Ag (II)
Измерения ЭДС и потенциометрическое титрование в среде ДМФ осуществляли при 20.0 ± 0.10С на рН-метре-милливольтметре METROHM-632 (Swiss made). Растворитель очищен и обезвожен по известным методикам [42, 47]. Содержание воды, определенное модифицированным методом К.Фишера [48], не превышало для ДМФ ±0.02 мас.%.
Для определения констант кислотности протонированного основания воспользуемся стандартным потенциалом E0 электрохимической цепи без переноса (II) [26] в соответствующем растворителе, величина которого используется для оценки активности иона лиония 
(а(SH+) в каждой точке титрования основания.
В табл. 5.5 приведены данные измерения ЭДС цепи (II) в среде ДМФ в зависимости от моляльной концентрации хлорной кислоты, выполненные с применением прибора METROHM-632 (Swissmade), а также результаты оценки степени диссоциации HClО4 и исходные величины для расчета стандартного потенциала цепи.
(4.10)
Величина 
, равная разности 
(
), определена по программе (Приложение II) по зависимости 
при lg m = 0. Получена величина = 0.3856 с коэффициентом регрессии r = 0.9981.
Таблица 5.5
Изменение ЭДС цепи (II) в зависимости от моляльной концентрации хлорной кислоты (m, моль HClO4/1000г ДМФ) в среде ДМФ и данные для определения стандартного потенциала цепи (II)
| m | E, B | α(HClO4) | -0.058×lg mα | (m×α)0.5 | E’ |
| 0.6834 | 0.382 | 0.1532 | 0.05684 | 0.32357 | 0.4388 |
| 0.3417 | 0.373 | 0.3947 | 0.05046 | 0.36728 | 0.4234 |
| 0.1708 | 0.366 | 0.6005 | 0.05736 | 0.32027 | 0.4233 |
| 0.0854 | 0.359 | 0.7363 | 0.06968 | 0.25076 | 0.4287 |
| 0.0427 | 0.348 | 0.7959 | 0.08518 | 0.18435 | 0.4332 |
| 0.02135 | 0.339 | 0.8541 | 0.10087 | 0.13504 | 0.4398 |
| 0.010675 | 0.330 | 0.8957 | 0.11713 | 0.09779 | 0.4471 |
Значение стандартного потенциала цепи (II) определено по компьютерной программе (Приложение II) по приближению функции 
при 
, где 
.
, r = 0.9992.
Таким образом, получена величина стандартного потенциала цепи (II) в среде ДМФ, равная Ео = 0.4607 В. Попутно отметим, что величина рКа (HClO4), полученная представленной выше разности, в среде ДМФ составляет
Стандартный потенциал цепи (II), наряду с равновесными концентрациями нейтральной молекулы основания и заряженных частиц 
, образующихся в процессе титрования оснований, и их коэффициентами активностей , дают возможность оценки термодинамических констант кислотности протонированных моно-, диоснований в среде органических растворителей.
Оценка активности лионий-ионов в процессе титрования основания возможна по уравнению Нернста:
.
Существенным отличием является определение равновесных концентраций свободного основания и протонированных форм , отличающееся от известных в литературе, основанных на использовании только первых ионов, является применение логарифмических диаграмм состояния молекул и ионов в титруемой системе (рис. 5.3-5.4), дающих возможность оценки концентраций любых частиц в титруемой системе.
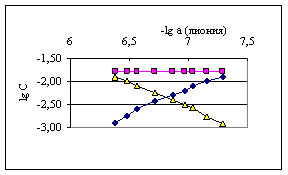
Рис. 5.3. Диаграмма -lg а (лиония) – lg C для определения равновесных концентраций 
- (-à-), 
- (-?-) и 
- (-Δ-) протонированного пара-фенилендиамина
Таблица 5.6
Расчет констант диссоциации пара-фенилендиамина в среде ДМФ по ур.(5.4)
| V, мл | Е, В | -lg a(SH+) | -lg [B] | -lg [BH+] | -lg [BH22+] | I0.5 | f1 | f2 | рК1 | рК2 |
| 1.0 | 0.046 | 7.291 | 1.90 | 1.79 | 2.92 | 0.1029 | 0.7184 | 0.2664 | 7.26 | 5.73 |
| 1.2 | 0.054 | 7.156 | 2.00 | 1.79 | 2.77 | 0.1077 | 0.7087 | 0.2523 | 7.22 | 5.72 |
| 1.4 | 0.061 | 7.037 | 2.10 | 1.79 | 2.58 | 0.1160 | 0.6920 | 0.2293 | 7.19 | 5.76 |
| 1.6 | 0.065 | 6.969 | 2.20 | 1.79 | 2.50 | 0.1205 | 0.6832 | 0.2179 | 7.22 | 5.76 |
| 1.8 | 0.071 | 6.868 | 2.30 | 1.79 | 2.40 | 0.1271 | 0.6707 | 0.2023 | 7.21 | 5.73 |
| 2.0 | 0.080 | 6.715 | 2.42 | 1.79 | 2.25 | 0.1394 | 0.6482 | 0.1766 | 7.16 | 5.69 |
| 2.2 | 0.089 | 6.563 | 2.60 | 1.79 | 2.10 | 0.1552 | 0.6213 | 0.1491 | 7.17 | 5.63 |
| 2.4 | 0.094 | 6.478 | 2.74 | 1.79 | 2.00 | 0.1679 | 0.6009 | 0.1304 | 7.21 | 5.60 |
| 2.6 | 0.100 | 6.376 | 2.89 | 1.79 | 1.90 | 0.1827 | 0.5786 | 0.1121 | 7.24 | 5.55 |
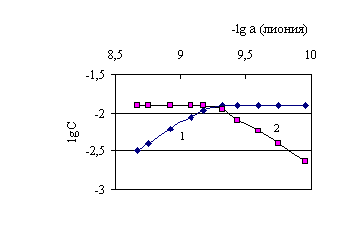
Рис. 5.4. Диаграмма -lg(активность лиония) – lg C для определения равновесных концентраций - (1) и - (2) протонированного дифенилгуанидина
В табл. 5.6 и 5.7 сведены все исходные данные для расчетов констант диссоциации по уравнению (5.4) при титровании 0.01639 н.раствора пара-фенилендиамина (табл. 5.6) и 0.01240 н. раствора дифенилгуанидина (табл. 5.7) и (титрант 0.08900 н. раствор пикриновой кислоты) в среде ДМФ.
Таблица 5.7
Расчет константы диссоциации протонированного дифенилгуанидина в среде ДМФ по ур.(5.4-верхняя часть)
| V, мл | -Е, В | -lg a(SH+) | -lg[B] | -lg[BH+] | I0.5 | f | pK |
| 0.7 | 0.115 | 9.957 | 1.90 | 2.64 | 0.03384 | 0.8905 | 9.17 |
| 1.0 | 0.103 | 9.750 | 1.90 | 2.41 | 0.04410 | 0.8610 | 9.18 |
| 1.2 | 0.094 | 9.595 | 1.90 | 2.24 | 0.05364 | 0.8350 | 9.18 |
| 1.4 | 0.085 | 9.439 | 1.90 | 2.09 | 0.06375 | 0.8087 | 9.16 |
| 1.6 | 0.078 | 9.319 | 1.90 | 1.95 | 0.07490 | 0.7813 | 9.16 |
| 1.8 | 0.070 | 9.181 | 1.96 | 1.90 | 0.07897 | 0.7716 | 9.12 |
| 2.0 | 0.064 | 9.077 | 2.06 | 1.90 | 0.07897 | 0.7716 | 9.12 |
| 2.2 | 0.055 | 8.922 | 2.21 | 1.90 | 0.07897 | 0.7716 | 9.11 |
| 2.4 | 0.045 | 8.750 | 2.40 | 1.90 | 0.07897 | 0.7716 | 9.13 |
| 2.5 | 0.040 | 8.664 | 2.50 | 1.90 | 0.07897 | 0.7716 | 9.14 |
Как видно из таблиц и рисунков, равновесные концентрации частиц, находящихся в титруемом растворе, вполне сопоставимы. Поэтому в расчетах рКа все концентрации должны быть учтены.
Результаты математической обработки значений рКа моно- и диоснований в среде ДМФ при числе экспериментальных точек от 7 до 12 по программе (Приложение IV) приводят к следующему доверительному интервалу с вероятностью 0.95: рКа1 и рКа2 пара-фенилендиамина/ДМФ = 7.21 ± 0.05 и 5.68 ±. 0.11, рКа (ДФГ/ДМФ) = 9.15 ± 0.03,.
Протонированные двухкислотные основания характеризуются близостью констант кислотности, подтверждаемой одним совместным скачком потенциала на кривых потенциометрического титрования, которые здесь мы не приводим.
Разработанная методика определения термодинамических констант кислотности протонированных моно- и диоснований (моно- и дикислот) в среде органических растворителей вполне приемлема при экспериментальном определении рКа любых одно- и двухкислотных оснований в диполярных апротонных растворителях.