Научная электронная библиотека

Взаимодействия в растворах электролитов: моделирование сольватационных процессов, равновесий в растворах полиэлектролитов и математическое прогнозирование свойств химических систем

Танганов Б. Б.,

4.1.5. Термодинамические константы трех- и четырехосновных кислот в органических растворителях

Концептуальный подход к оценке ионной силы раствора электролита заключался в полном учете концентраций всех равновесных частиц в титруемой системе. Отметим еще раз, что для сложных систем, к которым относится титруемый полиэлектролит, традиционно применялась концентрация только первого диссоциированного иона полиэлектролита, несмотря на присутствие двух- и многозарядных ионов, так как не было предложено реального инструмента, позволяющего количественно оценить продукты диссоциации.

В работе предложена модель оценки термодинамических констант диссоциации трехосновных кислот в среде органических растворителей на примере лимонной кислоты в этаноле при совместной нейтрализации функциональных групп [20].

Если константы диссоциации водных растворов одноосновных кислот могут быть определены при непосредственном измерении рН (активности ионов водорода), значительные трудности возникают при определении растворов многоосновных кислот при совместной нейтрализации кислотных групп, то есть при близости значений рК₁, pK₂,…, pK_n.

Экспериментальное определение рК даже одноосновных кислот в органических растворителях (где обычные рН теряют физический смысл), тем более поликислот, в связи с невозможностью прямого измерения активности лионий-ионов, представляет известную проблему.

Преобразуем уравнения (2.1) и (2.2) и рассмотрим диссоциацию трехосновной кислоты и соответствующие константы диссоциации в любом растворителе в упрощенном виде (без представления различных комплексов или сольватированных частиц, которые реально существуют в растворах):

(4.11)

, (4.12)

, . (4.13)

Для определения термодинамических констант диссоциации поликислот воспользуемся методами прямой потенциометрии и потенциометрического титрования, как наиболее наглядными и оптимальными среди известных методов. При этом требуется учитывать основные количественные законы теории растворов электролитов: закон электронейтральности, закон сохранения материального баланса, правило стехиометрии и ряд других.

Существующие методы оценок ионной силы при кислотно-основном равновесии основаны на использовании концентрации первой ионизированной частицы, например, для трехосновной кислоты. Ранее было показано, что пренебрегать равновесными концентрациями других ионов , и в расчетах констант диссоциации не следует, так как все они в процессе титрования становятся сопоставимыми. Наиболее плодотворным является представление кривой титрования любых электролитов (в том числе и кислот), как и в случае с моно- и дикислотами, в логарифмических координатах. Равновесные концентрации всех частиц , , , , образующихся при титровании поликислоты, определены на диаграммах -lg а(SH⁺) –lg C [7, 27, 30].

Оценка значения коэффициентов активности , , , проводится по предельному закону Дебая [8]:

(4.4)

или по уравнению Дэвиса [9]

, (4.5)

где , – ионная сила раствора, определяемая по известному уравнению:

а – расстояние наибольшего сближения ионов,

Полиэлектролиты, как правило, характеризуются близостью констант диссоциации. Поэтому определение значений последовательных констант равновесий затруднено.

Уравнения (4.11), (4.12) и (4.13) позволяют определить константы диссоциации электролитов как при дифференцированном титровании многоосновной кислоты, так и при совместной нейтрализации всех кислотных групп. Это становится возможным при экспериментальном определении стандартного потенциала электрохимической цепи без переноса [26]

Стеклянный электрод / НСl / AgCl, Ag (I)

или

Cтеклянный электрод / НСlО₄ / AgCl, Ag (II)

в соответствующих растворителях, величина которого () используется для оценки активности иона лиония при титрования полиэлектролита.

В табл. 4.12 приведены данные измерения ЭДС цепи (I) в среде этанола в зависимости от моляльной концентрации хлороводородной кислоты, приготовленной насыщением растворителя сухим хлористым водородом, а также результаты оценки степени диссоциации HCl и исходные величины для расчета стандартного потенциала цепи.

Таблица 4.12

Данные для расчета стандартного потенциала цепи (I)

m(HCl)	E_изм,В	α	0.059?lg(α?m)	(α?m)^1/2	E”
0.14710	0.350	0.3137	-0.07882	0.2148	0.4288
0.07355	0.344	0.5671	-0.08140	0.2042	0.4254
0.03677	0.332	0.6556	-0.09544	0.1553	0.4274
0.01834	0.320	0.7261	-0.11059	0.1155	0.4306
0.00919	0.307	0.7735	-0.12673	0.08433	0.4337
0.00459	0.291	0.7896	-0.14396	0.06025	0.4350
0.00230	0.276	0.8121	-0.16101	0.04320	0.4370

Величину определяют по линейной регрессии (Приложение I) при lg m = 0, получена величина -0,3898 В (коэффициент регрессии r = 0.9905).

Стандартный потенциал цепи (I), полученный по данным табл. 4.12 (последние столбцы) (Приложение II) равен Е_о = 0.4400 В.

4.1.5.1. Трехосновная кислота при совместной нейтрализации функциональных групп

Рассмотрим пример определения термодинамических констант диссоциации трехосновной (лимонной) кислоты в среде этилового спирта [20]. В табл. 4.13 приведена часть данных потенциометрического титрования 0.01585 н. раствора лимонной кислоты 0.03495 н. раствором гидроксида калия в этиловом спирте (V_iмл титранта, Е_изм, В), активности лионий-ионов (lg a) в процессе титрования, равновесные концентрации всех частиц ([H₃A], [H₂A^-], [HA²^-], [A³^-]) в титруемой системе, определяемые по рис. 4.15.

В следующей таблице (табл. 4.14) представлены ионная сила и коэффициенты активности ионов по уравнению Дэвиса (4.5), показатели последовательных констант диссоциации лимонной кислоты (pK_1, pK_2,pK₃) в среде этилового спирта и их статистически обработанные величины в буферных областях: для определения рК₁ 1.50 ± 0,.75 мл; для рК₂ 4.50 ± 0.75 мл; для рК₃ 7.50 ± 0.75мл:

рК₁ = 6.09 ± 0,03; рК₂ = 7.42 ± 0.04; рК₃ = 9.27 ± 0.03.

Применение уравнения Дэвиса при расчете коэффициентов активности ионов, образующихся при диссоциации трехосновной (лимонной) кислоты, более предпочтительно [38], так как доверительный интервал значительно меньше, чем при расчете констант по коэффициентам по Дебаю-Хюккелю. К тому же неопределенным является расстояние наибольшего сближения ионов, эмпирически выбираемое равным ~5?10⁻⁸см. Если учесть, что сумма радиусов одних и тех же сольватированных ионов в различных средах разная и значительно больше 5?10⁻⁸см, то значение а в уравнении (4.4) становится двусмысленным.

Таблица 4.13

Данные потенциометрического титрования 0.01585 н. раствора лимонной кислоты 0.03367 н. раствором гидроксида калия в среде этилового спирта и составляющие уравнений (4.11, (4.12) и (4.13) для расчетов рК₁, рК₂, рК₃

V_i	E, В	a(H₂M⁺)? 10⁷	[Н₃A] ?10³	[H₂A^-] ? 10³	[HA^2-]? 10³	[A³^-]? 10³	I^0,5
0.7	0.120	37.69	15.8	5.94	0.451	0.0106	0.0626
0.9	0.113	28.68	15.8	7.80	0.592	0.0139	0.0717
1.1	0.106	21.82	15.8	10.3	0.778	0.0182	0.0822
1.3	0.100	17.27	15.8	13.0	0.983	0.0231	0.0923
1.5	0.095	14.21	15.8	15.8	1.20	0.0280	0.1019
1.7	0.092	12.64	14.2	16.2	1.34	0.0315	0.1046
1.9	0.089	11.24	12.6	16.2	1.51	0.0354	0.1062
2.1	0.087	10.40	11.7	16.2	1.63	0.0383	0.1074
2.3	0.084	9.249	10.4	16.2	1.84	0.0430	0.1094
2.5	0.082	8.554	9.60	16.2	1.99	0.0465	0.1108
2.7	0.078	7.318	8.21	16.2	2.32	0.0544	0.1140
2.9	0.075	6.510	7.30	16.2	2.61	0.0612	0.1166
3.1	0.072	5.790	6.50	16.2	2.93	0.0688	0.1195
3.3	0.067	4.764	5.35	16.2	3.56	0.0836	0.1249
3.5	0.062	3.919	4.40	16.2	4.33	0.1020	0.1313
3.7	0.057	3.224	3.62	16.2	5.27	0.1230	0.1385
3.9	0.051	2.551	2.86	16.2	6.66	0.1560	0.1487
4.1	0.044	1.941	2.18	16.2	8.75	0.2050	0.1628
4.3	0.038	1.536	1.72	16.2	11.1	0.2590	0.1771
4.5	0.030	1.124	1.26	16.2	15.1	0.3540	0.1998
4.7	0.021	0.791	0.888	11.7	16.2	0.5030	0.2014
4.9	0.014	0.602	0.676	8.91	16.2	0.6610	0.1996
5.1	0.005	0.424	0.475	6.27	16.2	0.9390	0.1995
5.3	-0.003	0.310	0.348	4.59	16.2	1.2800	0.2012
5.5	-0.011	0.227	0.255	3.36	16.2	1.7500	0.2049
5.7	-0.016	0.187	0.210	2.76	16.2	2.1300	0.2083
5.9	-0.024	0.136	0.153	2.02	16.2	2.9100	0.2158
6.1	-0.027	0.121	0.136	1.80	16.2	3.2800	0.2192
6.3	-0.034	0.092	0.104	1.37	16.2	4.3000	0.2291
6.5	-0.040	0.073	0.082	1.08	16.2	5.4400	0.2397
6.7	-0.044	0.062	0.070	0.926	16.2	6.3600	0.2480
6.9	-0.048	0.053	0.060	0.792	16.2	7.4300	0.2574

Продолжение табл. 4.13

V_i	E, В	a(H₂M⁺)? 10⁷	[Н₃A] ?10³	[H₂A^-] ? 10³	[HA^2-]? 10³	[A³^-]? 10³	I^0,5
7.1	-0.055	0.041	0.046	0.603	16.2	9.7700	0.2769
7.3	-0.060	0.033	0.037	0.496	16.2	11.900	0.2934
7.5	-0.066	0.026	0.030	0.392	16.2	15.000	0.3165
7.7	-0.073	0.020	0.023	0.299	13.3	16.200	0.3159
7.9	-0.079	0.016	0.018	0.236	10.6	16.200	0.3069
8.1	-0.085	0.013	0.014	0.187	8.35	16.200	0.2996
8.3	-0.093	0.009	0.010	0.137	6.11	16.200	0.2920
8.5	-0.104	0.006	0.006	0.089	3.98	16.200	0.2846
8.7	-0.125	0.003	0.003	0.039	1.75	16.200	0.2766

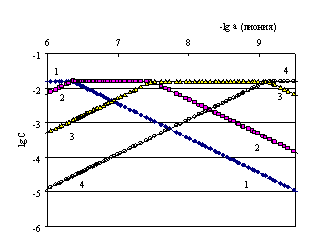
Рис. 4.15. Логарифмическая диаграмма lg a (лиония лимонной кислоты) – lg C.1 – [H₃А], 2 – [H₂A⁻], 3 – [HA²⁻], 4 – [A³⁻]

Как видно, все константы близки, ΔрК₁ = 7.42 – 6.10 = 1.32, ΔрК₂ = 9.28 – 7.42 = 1.86. Эти разности меньше 3, поэтому дифференцированное титрование лимонной кислоты, рассматриваемой как смесь трех кислот, не осуществлено.

Таким образом, разработана концепция теоретической оценки и экспериментального определения термодинамических констант диссоциации трехосновных кислот в среде органических растворителей при совместной нейтрализации всех кислотных групп.

Таблица 4.14

Коэффициенты активности по Дэвису [9], константы диссоциации лимонной кислоты с учетом коэффициентов активности по Дэвису

V_i	f₁ (4.5)	f₂ (4.5)	f₃ (4.5)	pK₁	pK₂	pK₃
0.7	0.6976	0.2368	0.0391	6.024	6.718	7.228
0.9	0.6679	0.1990	0.0264	6.047	6.860	7.370
1.1	0.6369	0.1645	0.0172	6.074	7.006	7.516
1.3	0.6094	0.1379	0.0116	6.100	7.133	7.643
1.5	0.5861	0.1180	0.0081	6.123	7.241	7.751
1.7	0.5800	0.1132	0.0074	6.119	7.260	7.808
1.9	0.5762	0.1102	0.0070	6.123	7.264	7.863
2.1	0.5734	0.1081	0.0067	6.126	7.267	7.900
2.3	0.5690	0.1048	0.0062	6.131	7.272	7.956
2.5	0.5659	0.1025	0.0059	6.134	7.275	7.993
2.7	0.5591	0.0977	0.0053	6.141	7.283	8.068
2.9	0.5536	0.0939	0.0049	6.148	7.289	8.125
3.1	0.5476	0.0899	0.00443	6.154	7.296	8.183
3.3	0.5367	0.0830	0.00370	6.167	7.309	8.281
3.5	0.5247	0.0758	0.00302	6.182	7.323	8.380
3.7	0.5116	0.0685	0.00240	6.198	7.340	8.481
3.9	0.4943	0.0597	0.00176	6.221	7.363	8.606
4.1	0.4725	0.0498	0.00117	6.252	7.394	8.756
4.3	0.4526	0.0419	0.00079	6.282	7.425	8.889
4.5	0.4246	0.0325	0.00045	6.329	7.473	9.072
4.7	0.4228	0.0319	0.00043	6.474	7.456	9.106
4.9	0.4248	0.0325	0.00045	6.589	7.452	9.102
5.1	0.4250	0.0326	0.00045	6.741	7.452	9.102
5.3	0.4229	0.0320	0.00043	6.880	7.456	9.106
5.5	0.4188	0.0308	0.00039	7.023	7.463	9.113
5.7	0.4151	0.0296	0.00036	7.115	7.470	9.120
5.9	0.4072	0.0275	0.00031	7.265	7.485	9.135
6.1	0.4036	0.0265	0.00028	7.323	7.492	9.142
6.3	0.3939	0.0241	0.00023	7.460	7.512	9.162
6.5	0.3841	0.0218	0.00018	7.582	7.532	9.182
6.7	0.3768	0.0202	0.00015	7.665	7.548	9.198

Продолжение табл. 4.14

V_i	f₁ (4.5)	f₂ (4.5)	f₃ (4.5)	pK₁	pK₂	pK₃
6.5	0.3841	0.0218	0.00018	7.582	7.532	9.182
6.7	0.3768	0.0202	0.00015	7.665	7.548	9.198
6.9	0.3690	0.0185	0.00013	7.751	7.566	9.216
7.1	0.3540	0.0157	0.00009	7.904	7.602	9.252
7.3	0.3424	0.0137	0.00006	8.018	7.632	9.281
7.5	0.3279	0.0115	0.00004	8.158	7.672	9.321
7.7	0.3282	0.0116	0.00004	8.276	7.756	9.320
7.9	0.3337	0.0124	0.00005	8.362	7.842	9.305
8.1	0.3384	0.0131	0.00006	8.452	7.931	9.292
8.3	0.3434	0.0139	0.00007	8.574	8.053	9.279
8.5	0.3485	0.0147	0.00008	8.653	8.131	9.272
8.7	0.3542	0.0157	0.00009	8.748	8.226	9.266

4.1.5.2. Трехосновная кислота при нейтрализации функциональных групп с двумя скачками титрования

Лимонная кислота титруется гуанидином в среде ДМФ с образованием двух скачков (рис. 4.16): 1-ый скачок соответствует нейтрализации первой карбоксильной группы, 2-ой - нейтрализации второй и третьей карбоксильных групп [21].

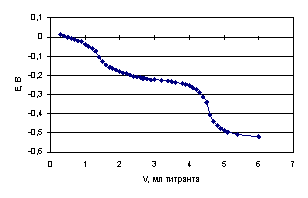
Рис. 4.16. Кривая потенциометрического титрования 0.02234 н. раствора лимонной кислоты 0.09985 н. раствором гуанидина в среде ДМФ

Данные потенциометрического титрования 0.02234 н. раствора лимонной кислоты 0.09985 н. раствором гуанидина в среде ДМФ и составляющие уравнений (4.11), (4.12) и (4.13) для расчетов констант диссоциации представлены в табл. 4.15.

Таблица 4.15

Данные для оценки термодинамических констант диссоциации лимонной кислоты в ДМФ

V_i_,мл	E_i, В	-lga(SH⁺)	[H₃A]	[H₂A⁻]	[HA²⁻]	[A³⁻]	I^0.5
0.5	-0.001	6.674	0.022340	0.013448	1.29·10^-5	1.84·10^-06	0.08221
0.6	-0.008	6.793	0.022340	0.017673	1.70·10^-5	2.42·10^-06	0.09424
0.7	-0.014	6.895	0.022340	0.022336	2.15·10^-5	3.05·10^-06	0.10594
0.8	-0.020	6.996	0.017680	0.022340	2.71·10^-5	3.86·10^-06	0.10602
0.9	-0.026	7.098	0.013989	0.022340	3.43·10^-5	4.88·10^-06	0.10611
1.0	-0.039	7.318	0.008422	0.022340	5.70·10^-5	8.10·10^-06	0.10640
1.1	-0.048	7.471	0.005928	0.022340	8.10·10^-5	1.15·10^-05	0.10669
1.2	-0.060	7.674	0.003711	0.022340	0.000129	1.84·10^-05	0.10729
1.3	-0.075	7.928	0.002067	0.022340	0.000232	3.30·10^-05	0.10855
1.4	-0.105	8.437	0.000641	0.022340	0.000749	0.000107	0.11466
1.5	-0.127	8.810	0.000272	0.022340	0.001767	0.000251	0.12584
1.6	-0.145	9.115	0.000135	0.022340	0.003567	0.000507	0.14348
1.7	-0.155	9.285	9.11·10⁻⁵	0.022340	0.005270	0.000750	0.15838
1.8	-0.165	9.454	6.16·10⁻⁵	0.022340	0.007786	0.001107	0.17812
1.9	-0.172	9.572	4.69·10⁻⁵	0.022340	0.010232	0.001455	0.19540
2.0	-0.180	9.708	3.43·10⁻⁵	0.022340	0.013982	0.001989	0.21927
2.1	-0.186	9.810	2.72·10⁻⁵	0.022340	0.017671	0.002513	0.24046
2.2	-0.192	9.911	2.15·10⁻⁵	0.022340	0.022333	0.003176	0.26482
2.3	-0.198	10.013	1.70·10⁻⁵	0.017682	0.022340	0.004015	0.26755
2.4	-0.204	10.115	1.35·10⁻⁵	0.013990	0.022340	0.005074	0.27296

Продолжение табл. 4.15

V_i_,мл	E_i, В	-lga(SH⁺)	[H₃A]	[H₂A⁻]	[HA²⁻]	[A³⁻]	I^0.5
2.5	-0.208	10.183	1.15·10⁻⁵	0.011968	0.022340	0.005931	0.27812
2.6	-0.211	10.233	1.02·10⁻⁵	0.010646	0.022340	0.006668	0.28285
2.7	-0.217	10.335	8.10·10⁻⁶	0.008423	0.022340	0.008427	0.29464
2.8	-0.219	10.369	7.49·10⁻⁶	0.007791	0.022340	0.009111	0.29929
2.9	-0.221	10.403	6.93·10⁻⁶	0.007206	0.022340	0.009851	0.30432
3.0	-0.223	10.437	6.41·10⁻⁶	0.006665	0.022340	0.010651	0.30974
3.2	-0.227	10.505	5.48·10⁻⁶	0.005702	0.022340	0.012450	0.32180
3.4	-0.230	10.556	4.88·10⁻⁶	0.005072	0.022340	0.013996	0.33196
3.5	-0.233	10.606	4.34·10⁻⁶	0.004511	0.022340	0.015735	0.34313
3.6	-0.237	10.674	3.71·10⁻⁶	0.003859	0.022340	0.018393	0.35969
3.8	-0.242	10.759	3.05·10⁻⁶	0.003175	0.022340	0.022340	0.38314

Продолжение табл. 4.15

V_i_,мл	f₁	f₂	f₃	pK₁	pK₂	pK₃
0.5	0.7523	0.5650	0.4244	7.018	−	−
0.6	0.7244	0.5236	0.3785	7.035	−	−
0.7	0.6988	0.4871	0.3395	7.050	−	−
0.8	0.6986	0.4868	0.3392	7.050	−	−
0.9	0.6984	0.4866	0.3390	7.050	−	−
1.0	0.6979	0.4857	0.3381	7.051	−	−
1.1	0.6972	0.4848	0.3372	7.051	−	−
1.2	0.6960	0.4831	0.3353	7.052	−	−
1.3	0.6933	0.4794	0.3315	7.054	−	−
1.4	0.6807	0.4620	0.3136	−	−	−

Продолжение табл. 4.15

V_i_,мл	f₁	f₂	f₃	pK₁	pK₂	pK₃
1.5	0.6587	0.4323	0.2837	−	−	−
1.6	0.6262	0.3903	0.2432	−	−	−
1.7	0.6008	0.3590	0.2144	−	−	−
1.8	0.5698	0.3224	0.1824	−	10.159	−
1.9	0.5449	0.2943	0.1590	−	10.179	−
2.0	0.5135	0.2607	0.1324	−	10.206	−
2.1	0.4882	0.2352	0.1133	−	10.229	−
2.2	0.4617	0.2098	0.0953	−	10.254	−
2.3	0.4589	0.2072	0.0935	−	10.257	−
2.4	0.4535	0.2021	0.0901	−	10.263	−
2.5	0.4484	0.1975	0.0870	−	10.268	−
2.6	0.4438	0.1934	0.0842	−	10.273	−
2.7	0.4328	0.1836	0.0779	−	10.284	−
2.8	0.4285	0.1799	0.0755	−	10.289	−
2.9	0.4241	0.1760	0.0731	−	10.294	11.141
3.0	0.4194	0.1720	0.0706	−	10.299	11.146
3.2	0.4092	0.1635	0.0653	−	−	11.157
3.4	0.4010	0.1568	0.0613	−	−	11.167
3.5	0.3924	0.1498	0.0572	−	−	11.177
3.6	0.3802	0.1403	0.0518	−	−	11.192
3.8	0.3642	0.1282	0.0451	−	−	11.212

Оценка равновесных концентраций всех частиц в титруемой системе осуществлена по данным диаграммы (рис. 4.17), значения которых приведены в табл. 4.15. По уравнениям (4.11), (4.12) и (4.13) и по данным табл. 4.15 рассчитаны термодинамические константы диссоциации (последние три колонки табл. 4.15).

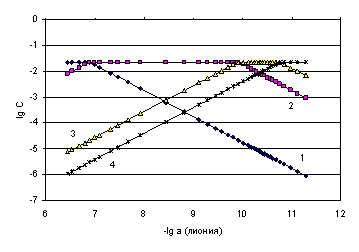
Рис. 4.17. Логарифмическая диаграмма «lg C – lg активности лиония» лимонной кислоты в ДМФ

Математическая обработка результатов расчетов (Приложение IV) приводит к доверительным интервалам:

рК₁= 7.04 ± 0.04; рК₂= 10.25 ± 0.09; рК₃ = 11.17 ± 0.05.

4.1.5.3. Четырехосновная кислота при нейтрализации функциональных групп с двумя скачками титрования

Четырехосновная этилендиаминотетрауксусная (ЭДТА) кислота в среде ДМФ титруется с двумя скачками потенциалов, причем первый скачок соответствует совместной нейтрализации первых двух карбоксильных групп, а второй – совместной нейтрализации остальных карбоксильных групп [7, 22, 27] (рис. 4.18).

В табл. 4.16 представлены данные потенциометрического титрования 2.3705·10⁻³ М раствора ЭДТА 5.04·10⁻² М раствором гуанидина в среде ДМФ, а также -lg a(SH⁺), логарифмы равновесных концентраций всех частиц в растворе в процессе титрования, определенных из рис. 4.19, их коэффициенты активности, рассчитанные по уравнению (4.5), рК_i исследуемой поликислоты по уравнению (2.2) для многоосновных кислот.

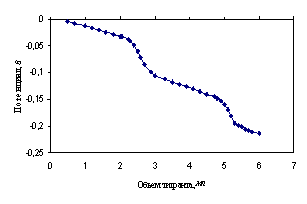
Рис. 4.18. Кривая потенциометрического титрования 3.37·10⁻³М раствора ЭДТА 0.0504М раствором гуанидина в ДМФ

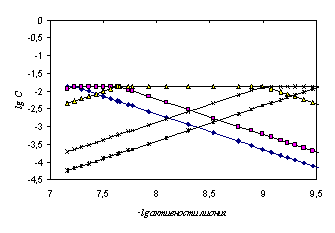
Рис. 4.19. Логарифмическая диаграмма «lg C – lg активности лиония» ЭДТА в ДМФ (à − [H₄A], − [H₃A⁻], Δ − [H₂A²⁻], х − [HA³⁻], * − [A⁴⁻])

Таблица 4.16

Данные для оценки термодинамических констант диссоциации ЭДТА в ДМФ

Vi	E, В	-lg a(SH⁺)	lg [H₄A]	lg [H₃A⁻]	lg [H₂A²⁻]	lg[HA³⁻]	lg[A⁴⁻]
0.5	-0.004	7.16	-1.8702	-1.9309	-2.3508	-3.7208	-4.2508
0.7	-0.008	7.23	-1.8773	-1.8702	-2.2830	-3.6530	-4.1830
1.0	-0.012	7.29	-1.9451	-1.8702	-2.2152	-3.5852	-4.1152
1.2	-0.016	7.36	-2.0129	-1.8702	-2.1474	-3.5174	-4.0474
1.4	-0.020	7.43	-2.0807	-1.8702	-2.0796	-3.4496	-3.9796
1.6	-0.024	7.50	-2.1485	-1.8702	-2.0118	-3.3818	-3.9118
1.8	-0.028	7.56	-2.2163	-1.8702	-1.9440	-3.3141	-3.8441
2.0	-0.032	7.63	-2.2841	-1.8702	-1.8763	-3.2463	-3.7763
2.2	-0.038	7.73	-2.3857	-1.9658	-1.8702	-3.1446	-3.6746
2.3	-0.040	7.77	-2.4196	-1.9997	-1.8702	-3.1107	-3.6407
2.4	-0.049	7.92	-2.5722	-2.1522	-1.8702	-2.9581	-3.4881
2.5	-0.059	8.09	-2.7417	-2.3217	-1.8702	-2.7886	-3.3186
2.6	-0.071	8.29	-2.9451	-2.5251	-1.8702	-2.5852	-3.1152
2.7	-0.085	8.53	-3.1824	-2.7624	-1.8702	-2.3480	-2.8780
2.9	-0.099	8.77	-3.4196	-2.9997	-1.8702	-2.1107	-2.6407
3.0	-0.106	8.89	-3.5383	-3.1183	-1.8702	-1.9920	-2.5220
3.3	-0.112	8.99	-3.6400	-3.2200	-1.8702	-1.8903	-2.4203
3.5	-0.117	9.07	-3.7247	-3.3048	-1.9347	-1.8702	-2.3356
3.7	-0.122	9.16	-3.8095	-3.3895	-2.0195	-1.8702	-2.2508
3.9	-0.126	9.23	-3.8773	-3.4573	-2.0873	-1.8702	-2.1830
4.1	-0.130	9.29	-3.9451	-3.5251	-2.1551	-1.8702	-2.1152
4.3	-0.135	9.38	-4.0298	-3.6098	-2.2398	-1.8702	-2.0305
4.5	-0.140	9.46	-4.1146	-3.6946	-2.3246	-1.8702	-1.9457
4.7	-0.145	9.55	-4.1993	-3.7793	-2.4093	-1.8793	-1.8702

Продолжение табл. 4.16

Vi	I^0.5	f₁	f₂	f₃	f₄	рК₁	рК₂
0.5	0.1268	0.6568	0.4298	0.2812	0.1840	7.40	8.13
0.7	0.1367	0.6383	0.4057	0.2579	0.1639	7.41	8.22
1.0	0.1439	0.6255	0.3893	0.2424	0.1509	7.42	8.25
1.2	0.1518	0.6117	0.3722	0.2264	0.1378	7.43	8.28
1.4	0.1607	0.5970	0.3543	0.2103	0.1248	7.44	8.31
1.6	0.1704	0.5816	0.3360	0.1941	0.1121	7.45	8.34
1.8	0.1811	0.5653	0.3172	0.1779	0.0998	7.46	8.38
2.0	0.1929	0.5483	0.2981	0.1621	0.0881	7.48	8.42
2.2	0.1931	0.5481	0.2978	0.1618	0.0879	7.42	8.43
2.3	0.1931	0.5481	0.2978	0.1618	0.0879
2.4	0.1950	0.5454	0.2949	0.1594	0.0862

Продолжение табл. 4.16

Vi	I^0.5	f₁	f₂	f₃	f₄	рК₃	рК₄
2.5	0.2012	0.5368	0.2855	0.1519	0.0807
2.6	0.2151	0.5187	0.2661	0.1366	0.0701
2.7	0.2421	0.4863	0.2333	0.1119	0.0537
2.9	0.2839	0.4427	0.1924	0.0836	0.0363
3.0	0.3118	0.4176	0.1705	0.0696	0.0284
3.3	0.3399	0.3948	0.1517	0.0583	0.0224	11.06	12.40
3.5	0.3479	0.3887	0.1469	0.0555	0.0210	11.09	12.47
3.7	0.3534	0.3847	0.1438	0.0537	0.0201	11.12	12.50
3.9	0.3601	0.3799	0.1401	0.0516	0.0190	11.15	12.54
4.1	0.3690	0.3737	0.1353	0.0490	0.0177	11.18	12.60
4.3	0.3832	0.3641	0.1282	0.0451	0.0158	11.24	12.68
4.5	0.4011	0.3529	0.1200	0.0408	0.0138	11.32	12.78
4.7	0.4185	0.3425	0.1127	0.0370	0.0122	11.39	12.88

Математическая обработка результатов, полученных при потенциометрическом титровании по термодинамическим константам диссоциации ЭДТА в среде ДМФ, приводит к доверительному интервалу, внутри которого с вероятностью 95% находятся показатели констант диссоциации (Приложение IV):

рК₁= 7.44 ± 0.06; рК₂= 8.31 ± 0.18;
рК₃ = 11.19 ± 0.19; рК₄ = 12.61 ± 0.26.

Из сравнения величин термодинамических констант диссоциации некоторых из одних и тех же электролитов, определенных в Главе 2 (раздел 2.1.1 − ЭДТА в ДМФ: табл.2.3 и 2.4; лимонная кислота в ДМФ: табл.2.7, 2.8; лимонная кислота в этаноле: табл. 2.6) и в Главе 4 (разделы 4.1.5.3 − ЭДТА в ДМФ, 4.1.5.2 − лимонная кислота в ДМФ, 4.1.5.1 − лимонная кислота в этаноле) можно сделать вывод о том, что они несколько расходятся, но применение логарифмических диаграмм для оценки рК_i более приемлемо. Во первых, доверительный интервал в большинстве обработанных величин более узок, что свидетельствует о достаточно высокой воспроизводимости результатов. Во вторых, учитываются равновесные концентрации всех частиц в системе в процессе переноса протона. В третьих, этот метод более нагляден и подтверждается диаграммами. В четвертых, при решении многих систем уравнений зачастую константы диссоциации оказываются отрицательными.

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

«Современные проблемы науки и образования» список ВАК ИФ РИНЦ = 1,006

«Фундаментальные исследования» список ВАК ИФ РИНЦ = 1,674

«Современные наукоемкие технологии» список ВАК ИФ РИНЦ = 0,940

«Успехи современного естествознания» список ВАК ИФ РИНЦ = 0,775

«Международный журнал прикладных и фундаментальных исследований» ИФ РИНЦ = 0,593

«Международный журнал экспериментального образования» ИФ РИНЦ = 0,425

«Научное Обозрение. Биологические Науки» ИФ РИНЦ = 0,400

«Научное Обозрение. Медицинские Науки» ИФ РИНЦ = 0,801

«Научное Обозрение. Экономические Науки» ИФ РИНЦ = 0,871

«Научное Обозрение. Педагогические Науки» ИФ РИНЦ = 0,733

«Научное Обозрение. Технические Науки» ИФ РИНЦ = 0,695

«European journal of natural history» ИФ РИНЦ = 0,301

«Международный студенческий научный вестник»

Издание научной и учебно-методической литературы ISBN РИНЦ DOI

РЕЦЕНЗИИ и ОТЗЫВЫ
кандидатов и докторов наук
на статьи, авторефераты, диссертации, монографии, учебники, учебные пособия

Академия Естествознания готовит к изданию реестр новых научных направлений, разработанных российскими учеными

Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

4.1.5. Термодинамические константы трех- и четырехосновных кислот в органических растворителях

Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания