Научная электронная библиотека

Краткий конспект лекций по начертательной геометрии

Пиралова О. Ф., Ведякин Ф. Ф.,

3.7. Пересечение прямой и плоскости

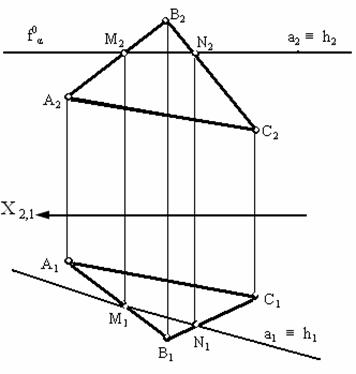
Линия пересечения двух плоскостей – прямая линия. Рассмотрим сначала частный случай (рис. 3.9), когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций (α π₁, f⁰_α Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π₁, (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).

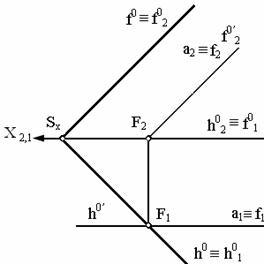
Если одна из плоскостей параллельна фронтальной плоскости проекций (рис. 3.9. б), то линия пересечения а, принадлежащая этой плоскости, будет параллельна плоскости π₂ и будет совпадать с фронталью пересекающихся плоскостей (а ≡ f).

Рис. 3.9. Частный случай пересечения плоскости общего положения с плоскостями: а – горизонтального уровня; б – фронтального уровня

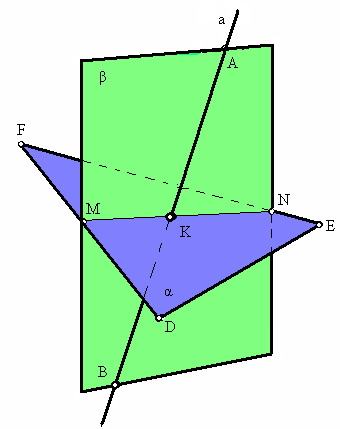
Пример построения точки пересечения (К) прямой а (АВ) с плоскостью α (DEF) показан на рис. 3.10. Для этого прямая а заключена в произвольную плоскость β и определена линия пересечения плоскостей α и β.

В рассматриваемом примере прямые АВ и MN принадлежат одной плоскости β и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости α (DEF), то точка К является и точкой пересечения прямой а (АВ) с плоскостью α. (рис. 3.11).

Рис. 3.10. Построение точки пересечения прямой с плоскостью

Для решения подобной задачи на комплексном чертеже необходимо уметь находить точку пересечения прямой общего положения с плоскостью общего положения.

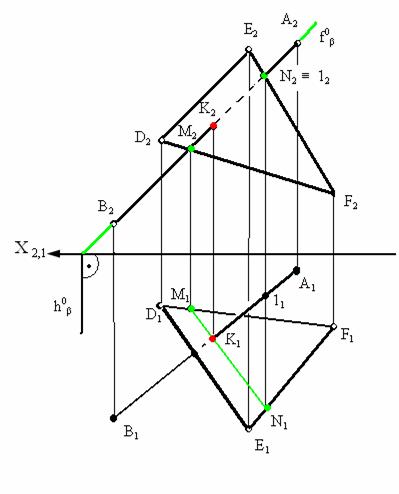
Рассмотрим пример нахождения точки пересечения прямой АВ c плоскостью треугольника DEF представленный на рис. 3.11.

Для нахождения точки пересечения через фронтальную проекцию прямой А₂В₂ проведена фронтально-проецирующая плоскость β которая пересекла треугольник в точках M и N. На фронтальной плоскости проекций (π₂) эти точки представлены проекциями M₂,N₂. Из условия принадлежности прямой плоскости на горизонтальной плоскости проекций (π₁) находятся горизонтальные проекции полученных точек M₁ N₁. В пересечении горизонтальных проекций прямых А₁В₁ и M₁N₁ образуется горизонтальная проекция точки их пересечения (К₁). По линии связи и условиям принадлежности на фронтальной плоскости проекций находится фронтальная проекция точки пересечения (К₂).

Рис. 3.11. Пример определения точки пересечения прямой и плоскости

Видимость отрезка АВ относительно треугольника DEF определена методом конкурирующих точек.

На плоскости π₂ рассмотрены две точки NEF и 1АВ. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (Y_N>Y₁ ), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К₁) закрыта плоскостью DEF на плоскости π₂(ее проекция К₂1₂ показана штриховой линии). Аналогично установлена видимость на плоскости π₁.