Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий конспект лекций по начертательной геометрии

Пиралова О. Ф., Ведякин Ф. Ф.,

6.3. Задачи на определение действительных величин плоских геометрических фигур и углов между ними

Общей схемой решения задач этой группы является приведение заданной плоской фигуры или плоскости угла в положение, параллельное одной из плоскостей проекций.

При выборе способа преобразования комплексного чертежа следует стремиться к простоте графических операций, их четкости и наименьшему количеству. Наиболее часто при решении задач применяются способы замены плоскостей проекций и вращения вокруг линии уровня. Способ вращения вокруг линии уровня является наиболее целесообразным для решения большинства задач данной группы, так как дает решение путем одного преобразования комплексного чертежа. К задачам данной группы можно отнести:

3адача 1. Определение действительной величины плоской фигуры. Решение задачи дано на рис. 5.4, 5.5, лекции 5. Задача решается аналогично задаче 1.

Задача 2. Определение угла, образованного двумя пересекающимися прямыми.

Задача 3. Определение величины угла, образованного прямой и плоскостью.

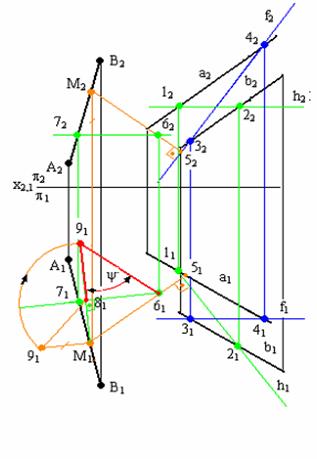
Углом между прямой и плоскостью называется угол между этой прямой и ее прямоугольной проекцией на данную плоскость. Решение задачи приведено на рис. 6.4.

Для определения угла между прямой АВ и плоскостью ∑ (а || b) необходимо:

1. Определить направление горизонтальной проекции горизонтали h₁ и фронтальной проекции фронтали плоскости ∑ (а || b).

2. Из произвольной точки М, принадлежащей прямой АВ (МАВ) провести прямую М₂5₂ f₂ и М₁5₁h₁.

.

Рис. 6.4. Определение величины угла, образованного прямой и плоскостью.

3. Определить величину угла y вращением его вокруг горизонтали до положения, параллельного плоскости П_1.

4. Вычислить значение искомого угла φ = 90⁰ - Ψ⁰

Задача 4. Определение величины угла между двумя пересекающимися плоскостями.

Мерой угла между двумя плоскостями служит линейный угол, образованный двумя прямыми – сечениями граней этого угла плоскостью, перпендикулярной к их ребру.

В задаче необходимо линию пересечения АВ плоскостей ∑ и Γ преобразовать в прямую уровня, а затем в линию проецирующую.

Общей схемой решения задач на построение в плоскости общего положения геометрических фигур по заданным размерам является:

1) преобразование заданной плоскости общего положения в плоскость уровня;

2) решение в плоскости уровня заданной метрической задачи.

Вопросы для самоконтроля

1. Как нужно располагать дополнительные плоскости проекций, чтобы прямую общего положения преобразовать в: а) прямую уровня; б) проецирующую прямую.

2. Как нужно располагать дополнительные плоскости проекций, чтобы плоскость общего положения преобразовать в: а) проецирующую; б) плоскость уровня?

3. Какие основные метрические задачи можно решать с помощью дополнительного проецирования?

4. Какие метрические задачи относят к основным?