
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
10.1. Основные положения
Касательные плоскости имеют большое значение в начертательной геометрии. Наличие касательных плоскостей позволяет определить направление нормали n к поверхности в точке касания М. Решение таких задач находит широкое применение в инженерной практике. С помощью касательных плоскостей выполняют построение очерков геометрических фигур, ограниченных замкнутыми поверхностями.
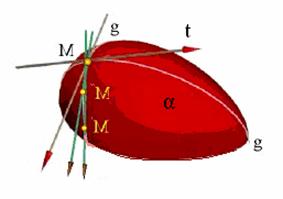
Прямая линия t, касательная к какой-либо кривой линии g, принадлежащей поверхности, является касательной и к поверхности (Рис. 10.1, а).
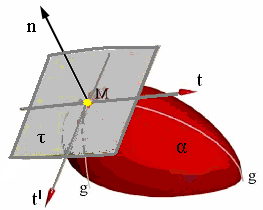
Нормалью к поверхности в заданной точке называется прямая, которая перпендикулярна к касательной плоскости τ и проходящая через точку касания (Рис. 10.1, б).
Плоскость, касательная к поверхности в заданной на поверхности точке М, есть множество всех прямых − касательных, проведенных к поверхности через данную точку. Через любую точку поверхности можно провести множество кривых, а, следовательно, и множество касательных прямых. Положение плоскости в пространстве определяется двумя пересекающимися прямыми, поэтому для построения касательной плоскости к поверхности в заданной точке достаточно построить касательные к двум кривым линиям, проходящим через эту точку. В качестве таких кривых выбирают наиболее простые линии поверхности. Если данная поверхность является линейчатой, то за одну из таких кривых целесообразно взять прямолинейную образующую (касательная к прямой линии есть сама прямая).
В дифференциальной геометрии доказывается, что все эти касательные прямые располагаются в одной плоскости, которая называется касательной плоскостью (τ) к поверхности в данной ее точке (рис. 10.1, б).
Если через точку поверхности можно провести касательную плоскость и при том одну, то точка поверхности называется о б ы к н о в е н н о й, в другом случае − о с о б о й (например, вершина конической поверхности).
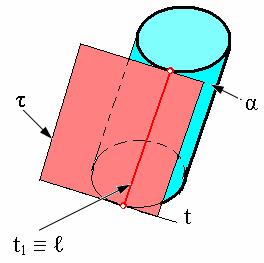
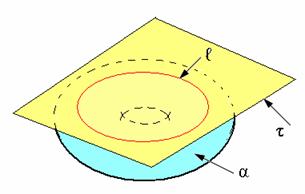
Касательная плоскость и кривая поверхность могут занимать различные положения относительно друг друга. При этом общим элементом может быть только элемент касания: либо точка М (рис. 10.1), либо линия (рис. 10.2). Эта линия может прямой (рис. 10.2, а) или кривой (рис. 10.2, б).
При построении касательной плоскости либо указывают точку касания, либо задают другие условия для ее проведения (например: касательная плоскость должна проходить через заданную вне поверхности точку; касательная плоскость должна быть параллельна некоторой прямой и др.).
 .
.
а
 .
.
б
Рис. 10.1. Касательные к поверхности α: а − прямая t , б − плоскость
 .
.
а
 .
.
б
Рис. 10.2. Изображение касательных линий: а − прямая, б − кривая
