
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2 Дифференциальное уравнение неравномерного движения потока
Уравнение неравномерного движения дает возможность рассчитать и построить кривую свободной поверхности потока.
Для вывода уравнения рассмотрим продольный разрез потока, находящегося в состоянии неравномерного движения (рисунок 3.2). Составим уравнение Бернулли для двух сечений 1–1 и 2–2, удаленных на бесконечно малом друг от друга расстоянии, предполагаем, что расход Q = const (вдоль потока):
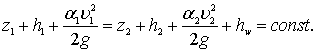 (3.2)
(3.2)
Уравнение (3.2) представим в следующем виде:
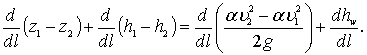 (3.3)
(3.3)
В этом уравнении
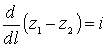 – представляет собой уклон дна;
– представляет собой уклон дна;
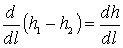 – изменение глубины на отрезке dl, то есть уклон свободной поверхности (пьезометрический уклон Iр);
– изменение глубины на отрезке dl, то есть уклон свободной поверхности (пьезометрический уклон Iр);
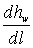 – потери напора (энергии) на участке dl, то есть гидравлический уклон I.
– потери напора (энергии) на участке dl, то есть гидравлический уклон I.
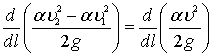 – изменение кинетической энергии на участке dl, которое можно представить следующим образом:
– изменение кинетической энергии на участке dl, которое можно представить следующим образом:
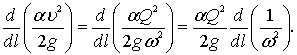
Площадь живого сечения ω зависит от двух координат ω=f(h, l), то есть
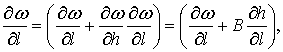 (3.4)
(3.4)
где 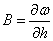 ширина потока поверху (рисунок 3.3).
ширина потока поверху (рисунок 3.3).
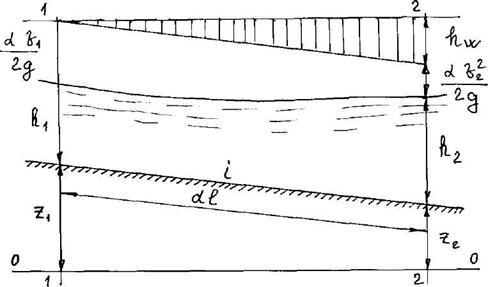
Рисунок 3.2 Схема к выводу уравнения неравномерного движения
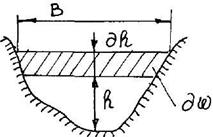
Рисунок 3.3
С учетом выражения (3.4) изменение кинетической энергии запишется
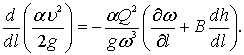 (3.5)
(3.5)
В уравнении (3.3) 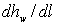 – потери напора (энергии) на участке dl, то есть гидравлический уклон I. Величину гидравлического уклона можно получить из формулы Шези
– потери напора (энергии) на участке dl, то есть гидравлический уклон I. Величину гидравлического уклона можно получить из формулы Шези
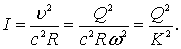
Подставим полученные выше выражения в уравнение (3.2)
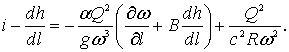
Решая это уравнение относительно 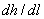 , получим
, получим
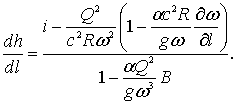 (3.6)
(3.6)
Уравнение (3.6) называется дифференциальным уравнением неравномерного движения в общем виде. Это уравнение относится к общему случаю непризматического русла. При помощи этого уравнения можно получить приращение глубины потока на элементарной длине его dl
