Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

3.5 График удельной энергии сечения

Анализ уравнения (З.11) показывает, что при постоянном расходе Q удельная энергия сечения зависит только от глубины h, так как ω = f(h). Это дает возможность построить график удельной энергии сечения (рисунок 3.5).

Из уравнения (3.11) следует, что:

а) при h → 0, E_П → 0, Е_К → ∞, следовательно, Е → ∞;

б) при h → ∞, E_П → ∞, Е_К → 0, и Е → ∞ то есть функция Е_сеч = f(h) имеет минимум при некоторой глубине h_кр.

Глубина потока, при которой удельная энергия сечения имеет минимальное значение, называется критической глубиной

График удельной энергии сечения дает возможность оценить энергетическое состояние потока.

Экстремальная точка на графике (рисунок 3.5), соответствующая h = h_кр, делит кривую удельной энергии на две части: верхнюю, где h > h_кр, и нижнюю, где h < h_кр. Соответственно принято различать три состояния потока:

1) спокойное состояние при h > h_кр; в этом случае удельная энергия сечения увеличивается с увеличением h;

2) бурное состояние потока при h < h_кр, удельная энергия сечения уменьшается с увеличением h;

3) критическое состояние потока, при котором глубина потока равна критической h = h_кр

Значение критической глубины необходимо не только для определения состояния потока, но и для выполнения ряда гидравлических задач.

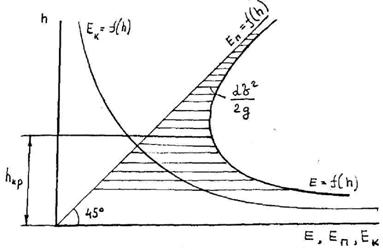
Рисунок 3.5 График удельной энергии сечения