Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.9 Формы свободной поверхности потока в призматических руслах с прямым уклоном дна (i > 0)
Формы кривых свободной поверхности потока могут быть получены при анализе уравнения неравномерного установившегося движения для призматического русла.
Выполним в числителе и знаменателе уравнения (3.7) некоторые преобразования;
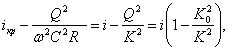 (3.21)
(3.21)
где К0 – расходная характеристика при равномерном движении потока при заданном расходе Q;
К – расходная характеристика при неравномерном движении.
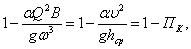 (3.22)
(3.22)
где ПК – параметр кинетичности.
С учетом выполненных преобразований уравнение неравномерного движения (3.7) примет вид
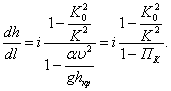 (3.23)
(3.23)
Проведем анализ возможных форм свободной поверхности для наиболее часто встречающегося в практике лесосплава случая – водотока с прямым уклоном дна (i > 0) [5].
При этом возможны три варианта:
1) i < iкр, h0 > hкр, ПК < 1 – поток находится в бурном состоянии;
2) i = iкр, h0 = hкр, ПК = 1 – – поток находится в критическом состоянии;
3) i > iкр, h0 < hкр, ПК > 1 – – поток находится в спокойном состоянии.
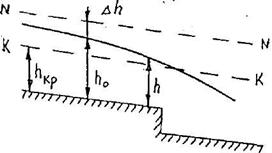
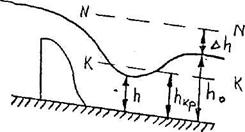
Вариант 1 i > 0, i < iкр, h0 > hкр, то есть поток находится в спокойном состоянии. При неравномерном движении здесь возможны три зоны: "а" – глубина h > h0 ,"в" – глубина h0 > h > hкр и "с" – глубина h < hкр (рисунок 3.6).
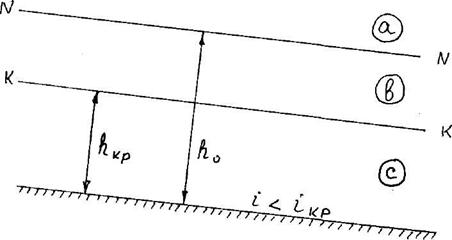
Рисунок 3.6
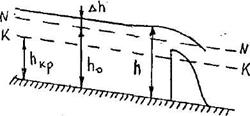
Кривая aI. Для зоны "а" глубина потока h > h0 > hкр. Так как h > h0, то и К > K0, следовательно, в уравнении (3.23) числитель больше нуля. Так как Пк < 1, то dh/dl > 0, то есть глубина потока возрастает вниз по течению, то есть получим кривую подпора типа aI (рисунок 3.7).
При стремлении h к бесконечности K → ∞, а ПК → 0 и dh/ds → i, то есть в низовой своей части кривая свободной поверхности приближается к горизонтальной прямой (рисунок 3.7).
При стремлении h → h0 (левая часть кривой подпора aI), 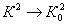 , а поэтому dh/dl → 0, следовательно, в верховой части кривая aI будет иметь асимптоту в виде линии N – N, характеризуемой условием dh/dl = 0. Так как кривая aI асимптотически приближается к прямой N – N, то подпор, вызываемый гидротехническим сооружением, распространяется вверх по течению теоретически па бесконечно большую длину.
, а поэтому dh/dl → 0, следовательно, в верховой части кривая aI будет иметь асимптоту в виде линии N – N, характеризуемой условием dh/dl = 0. Так как кривая aI асимптотически приближается к прямой N – N, то подпор, вызываемый гидротехническим сооружением, распространяется вверх по течению теоретически па бесконечно большую длину.

Рисунок 3.7 Кривая подпора типа aI
В практических расчетах пренебрегают некоторой малой величиной Δh, равной (0.01…0.02) h0, и считают длину кривой подпора конечной.
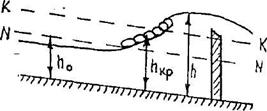
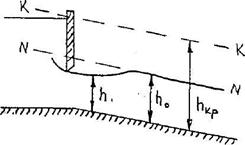
Кривая bI. Для зоны "в" глубина потока h0 > h > hкр, i < iкр. Так как h < h0, то K < K0 и 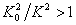 , числитель меньше нуля. Так как Пк < 1, то знаменатель положителен, глубина потока уменьшается по течению, то есть получаем кривую спада типа bI (рисунок 3.8).
, числитель меньше нуля. Так как Пк < 1, то знаменатель положителен, глубина потока уменьшается по течению, то есть получаем кривую спада типа bI (рисунок 3.8).
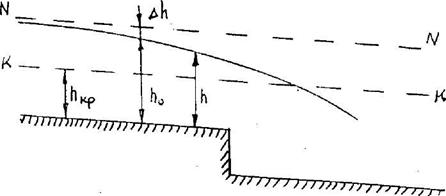
Рисунок 3.8 Кривая спада типа bI
При стремлении h → h0 величина 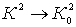 , а следовательно,
, а следовательно, 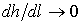 , то есть B в левой своей части имеет асимптоту в виде линии N – N.
, то есть B в левой своей части имеет асимптоту в виде линии N – N.
При стремлении h → hкр, Пк → 1 и 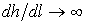 , то есть свободная поверхность кончается водопадом.
, то есть свободная поверхность кончается водопадом.
Кривая спада типа bI устанавливается в каналах перед перепадами, а в равнинных реках перед порогами, водопадами и т.п.
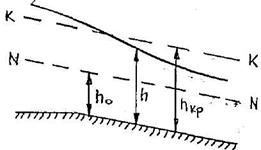
Кривая cI. Для зоны "с" глубина потока h < hкр < h0, i < iкр. Так как h < h0, то К < K0 и Пк > 1, числитель и знаменатель в формуле (3.23) будут отрицательными, следовательно, 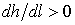 , глубина потока возрастает вниз по течению, т.е. имеет место кривая подпора типа cI (рисунок 3.9).
, глубина потока возрастает вниз по течению, т.е. имеет место кривая подпора типа cI (рисунок 3.9).
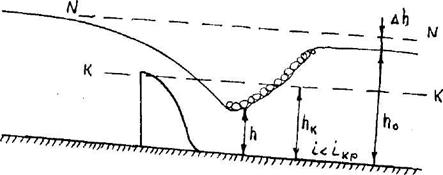
Рисунок 3.9 Кривая подпора типа С1
При h → hкр, Пк → 1, то есть 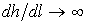 , и кривая свободной поверхности в нижней части стремится к вертикальной линии, то есть заканчивается прыжком.
, и кривая свободной поверхности в нижней части стремится к вертикальной линии, то есть заканчивается прыжком.
Таблица 3.1 Типы кривых свободной поверхности
| Вариант I | Вариант II |
| h > h0 > hкр Кривая подпора типа аI | h > hкр > h0 Кривая подпора типа аII |
| h0 > h > hкр Кривая подпора типа bI | hкр > h > h0 Кривая подпора типа bII |
| h < hкр < h0 Кривая подпора типа cI | h < h0< hкр Кривая подпора типа cII |
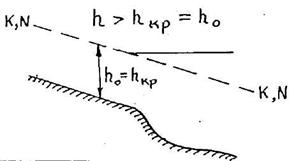
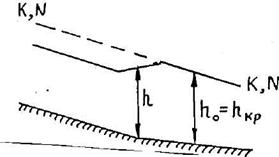
| Вариант III i > 0, i = iкр, h0 = hкр | |
| h > hкр = h0 Кривая подпора типа aIII | Кривая подпора типа cIII |
Кривая типа сI встречается при сопряжении сжатой струи ниже плотины с потоком в нижнем бьефе, при истечении из под щита в водотоках с малым уклоном дна.
Вариант 2. i > 0, i > iкр, h0 < hкр, поток находится в бурном состоянии. Анализ уравнения (3.23), проводимый точно так же, как и в первом варианте, показывает, что в канале может иметь место одна из трех кривых свободной поверхности типа aII, bII, cII (таблица 3.1).
Вариант 3. i > 0, i = iкр, h0 = hкр, в этом случае зона "в" исчезает, соответственно получаем две кривые свободной поверхности: кривые подпора типа aIII и cIII (таблица 3.1).
Не делая анализа уравнения (3.23) для случая i = 0 и i < 0, отметим, что кривые свободной поверхности имеют два основных типа: выпуклая кривая спада b0, 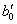 и вогнутая кривая подпора c0,
и вогнутая кривая подпора c0, 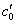 . Эти случаи встречаются на практике сравнительно редко (рисунок 3.10, рисунок 3.11).
. Эти случаи встречаются на практике сравнительно редко (рисунок 3.10, рисунок 3.11).
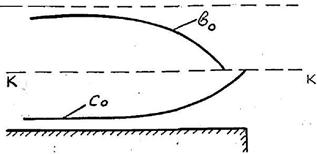
Рисунок 3.10 Форма кривой свободнойповерхности при i = 0
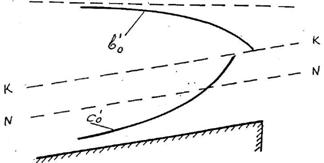
Рисунок 3.11 Форма кривой свободной поверхности при i < 0