Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

3.11 Интегрирование дифференциальных уравнений установившегося неравномерного движения в открытых призматических руслах

Для построения кривой свободной поверхности в призматических руслах необходимо проинтегрировать дифференциальное уравнение (3.23).

К настоящему времени имеется несколько методов интегрирования этого уравнения: метод Бресса, применяемый для русел прямоугольного сечения с очень большой шириной [6]; графический метод; метод последовательских приближений; метод Бахметьева Б.А. и др. Однако наибольшее применение нашел способ Б.А.Бахметьева, который применим для большинства русел правильного поперечного сечения, встречающихся в практике.

Б.А. Бахметьев предложил для интегрирования уравнения (3.23) в случае i > 0 использовать показательную зависимость

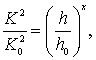  (3.24)

где  x – называется гидравлическим показателем русла;

h – действительная глубина в рассматриваемом поперечном сечении;

h₀ – нормальная глубина, определяемая по формуле Шези;

К, К₀ – модули расхода, отвечающие этим глубинам.

Логарифмируя (3.24), получим

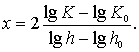  (3.25)

Модуль расхода определен точно для некоторых типов русел: весьма узкие прямоугольные, х = 2,0; широкие прямоугольные, х = 3,4; узкие параболические, х = 3,7; широкие параболические, х = 4,4; треугольные, х = 5,4.

Для трапецеидального русла

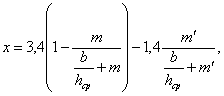  (3.26)

где  b – ширина русла по дну;

m – коэффициент откоса;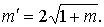 

Рассмотрим интегрирование уравнения (3.23) по методу Б.А.Бахметьева

1. Уклон дна i > О

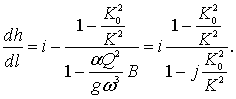  (3.27)

Введем дополнительное обозначение

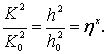  (3.28)

где  h/h₀ – относительная глубина, откуда h = ηh₀ или

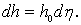
Учитывая принятое обозначение (3.28), уравнение (3.27) запишется

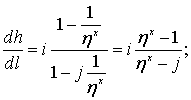 (3.29)

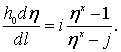
Разделяя переменные, получим

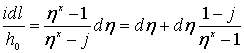 (3.30)

или

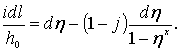
Прежде чем проинтегрировать уравнение (3.30), рассмотрим продольный разрез потока (рисунок 3.14) и выделим часть потока  сечениями 1–1 и 2–2. Обозначим:

 l – длина кривой свободной поверхности между сечениями;

 h₁, h₂ – глубина потока в верхнем и нижнем сечениях потока;

 h₀ – нормальная глубина.

Дифференциальное уравнение было составлено для произвольной элементарной части потока длиной dl. Интегрируя уравнение (3.30) от сечения 1–1 до сечения 2–2, получим

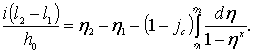 (3.31)

Считая, что для данного русла х = const; подынтегральную функцию в уравнении (3.31) следует рассматривать как функцию только η. Поэтому можно записать

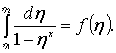  (3.32)

Окончательно уравнение кривой свободной поверхности запишется

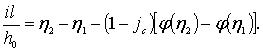  (3.33)

В этом уравнении

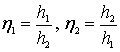 – относительные глубины в соответствующих сечениях;

 j₁, j₂ – коэффициент изменения кинетической энергии;

 j_c0,5(j₁+j₂) – вычисляются по зависимости соответствен  но для глубин h₁ и h₂.

Величины 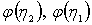 были вычислены путем разложения подынтегральной функции (3.32) в ряд для различных значений η и x. Результаты вычислений сведены в таблицу [6], [16].

Пользуясь уравнением (3.33), можно решить следующие задачи:

1) известна глубина h₁ (или h₂), требуется определить глубину h₂ (или h₁) в сечении потока, расположенном на заданном расстоянии l от сечения с глубиной h₁ (или h₂);

2) известны h₁ и h₂, требуется определить расстояние l между сечениями с заданными глубинами;

3) известны глубины h₁ и h₂, требуется построить кривую свободной поверхности АВ.

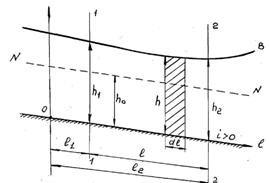
Рисунок 3.14 Продольный разрез потока

2. Обратный уклон дна i < 0.

В этом случае уравнение неравномерного движения для построения кривой свободной поверхности запишется

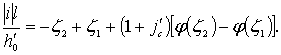  (3.34)

В случае i < 0 действительные элементы потока h, К мы заменяем элементами фиктивного равномерного потока 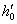 и .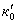

В уравнении (3.34) j_c – среднее значение, определяемое по формуле

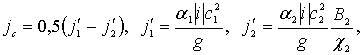
где 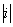 – абсолютная величина уклона;

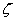  – относительная глубина,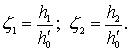 

Функции 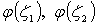 определяются по таблице [5], [16].

3. Уклон дна i = 0.

Уравнение неравномерного движения для построения кривой свободной поверхности в случае i = 0 (рисунок 3.15) имеет вид

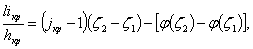  (3.35)

где h_кр – критическая глубина;

 i_кр – критический уклон; 

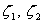  – относительная глубина,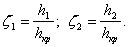 

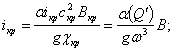
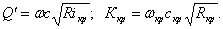
при i < 0 и i = 0

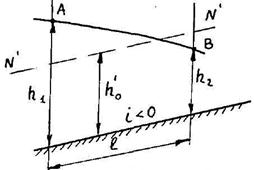
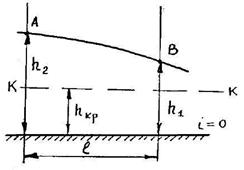
Рисунок 3.15 Кривые свободной поверхности