Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

3.12 Построение кривой свободной поверхности потока по уравнению Бернулли

Кривая свободной поверхности потока в непризматическом русле может быть построена с использованием уравнения Бернулли.

Предположим, что нам заданы: тип русла, уклон дна i, расход Q, глубина потока перед гидротехническим сооружением h_г или глубина потока в начальном сечении подпора (рисунок 3.16).

Для построения кривой свободной поверхности АВ разбиваем сечениями длину распространения кривой L на отдельные участки длиной l.Запишем уравнение Бернулли, например, для сечений 1 – 1 и 2 – 2 относительно плоскости сравнения 0 – 0 [14], [15]

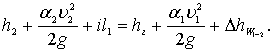  (3.36)

где 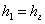– глубина потока перед гидротехническим сооружением;

 il₁ – падение дна русла от сечения 1 – 1 до сечения 2 – 2;

 υ₁, υ₂ – средние скорости в соответствующих сечениях;

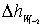 – потери напора по длине от сечения 2 – 2 до сечения 1 – 1, которые можно определить по зависимости

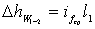,  (3.37)

где 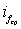 – среднее значение уклона трения на участке l₁.

Уклон трения определяется по формуле [5]

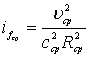,  (3.38)

где 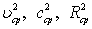 – гидравлические элементы потока, определенные для некоторого среднего сечения, расположенного между сечениями 2–2 и 1–1, и для некоторой средней глубины .

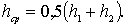Средний уклон трения может быть определен по формуле

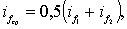
где  – уклоны трения, найденные для глубин h₁ и h₂

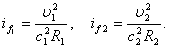
В уравнении Бернулли (3.36) обозначим через Е₂ и Е₁ удельные энергии в соответствующих сечениях, то есть

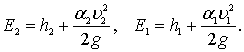
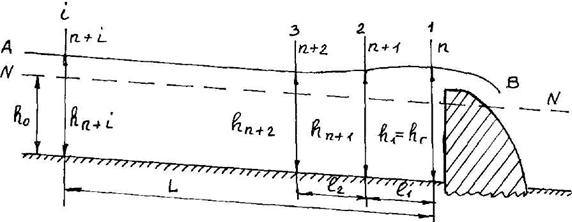
Рисунок 3.16 К построению кривой свободной поверхности

Подставляя Е₂, Е₁ (3.37) в уравнении (3.36), получим

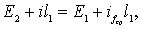
откуда

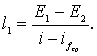  (3.39)

Это и есть основное уравнение Бернулли для построения кривой свободной поверхности.

Рассмотрим метод построения кривой свободной поверхности с использованием уравнения (3.39).

Расчет можно выполнить, идя вниз или вверх по течению. Применительно к рисунку 3.16 рассмотрим метод расчета, идя вверх по течению.

Пусть задана глубина перед гидротехническим сооружением 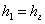. Определяется расстояние l₁ от сечения 1–1 с глубиной h_г до сечения 2–2 с глубиной h_n+1 по уравнению (3.39). При этом глубина h_n > h_n+1 на величину Δh₁. В расчетах разность глубин h_г – h_n можно разбивать на равные промежутки Δh или принимать для каждой пары сечений произвольно. Затем, считая глубины  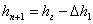и 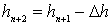 известными, определяется расстояние l₂. Значения Δh₁, Δh₂ имеют знак минус, так как в рассматриваемом случае глубина уменьшается от h_г до h₀.

Уравнение (3.39) является основным расчетным уравнением для русла с прямым уклоном дна i > 0. В случае горизонтального русла в уравнении (3.39) принимаем i = 0, а в случае обратного уклона i < 0, принимаем i = |i|, где |i| – абсолютная величина уклона.

Описанный выше общий метод расчета и построения кривой свободной поверхности в нецилиндрическом русле может быть использован и для любого цилиндрического русла.