
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.2.1 Общий вид уравнения неравномерного установившегося движения при установке в русле реки поперечной запани
Уравнение неравномерного установившегося движения потока в русле реки при установке в нем поперечной запани может быть получено из уравнения Бернулли, записанного для сечений 1–1 и 2–2 относительно плоскости сравнения 0–0 (рисунок 4.5) [18]
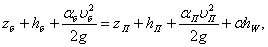 (4.1)
(4.1)
где hб, υб – соответственно глубина и скорость потока в бытовом состоянии;
hП, υП – глубина и скорость потока после установки поперечной запани;
zб, zП – положение рассматриваемых сечений относительно плоскости сравнения;
αhW – потери напора (энергии) на расстоянии;
αб, αП – безразмерный коэффициент, представляющий отношение действительной кинетической энергии потока с пыжом к энергии, вычисленной по средней скорости [19].
Разделив члены уравнения (4.1) на dl и сделав преобразование, получим
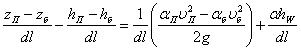 , (4.2)
, (4.2)
В этом уравнении
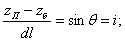 (4.3)
(4.3)
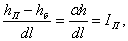 (4.4)
(4.4)
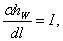 (4.5)
(4.5)
где I, IП, i – соответственно уклон дна, пьезометрический и гидравлический уклоны.
Значение гидравлического уклона (4.5) может быть определено из уравнения Шези [5], предполагая, что поток находится в состоянии равномерного движения
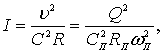 (4.6)
(4.6)
где сП – опытный коэффициент Шези для потока с пыжом;
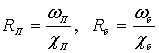 ,
,
где 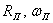 и
и 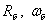 – гидравлический радиус, площадь живого сечения потока с пыжом и в бытовом состоянии;
– гидравлический радиус, площадь живого сечения потока с пыжом и в бытовом состоянии;
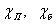 – смоченный периметры потока с пыжом и в бытовом состоянии.
– смоченный периметры потока с пыжом и в бытовом состоянии.
Введя обозначения 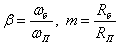 в формулу (4.6), получим
в формулу (4.6), получим
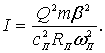 (4.7)
(4.7)
В уравнении (4.2) изменение кинетической энергии может быть представлено следующим образом:
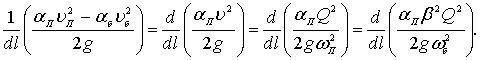 (4.8)
(4.8)
Учитывая, что 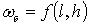 , запишем выражение (4.8) в частных производных
, запишем выражение (4.8) в частных производных
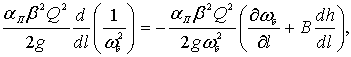 (4.9)
(4.9)
где 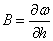 – ширина потока по урезу воды.
– ширина потока по урезу воды.
Подставляя выражение 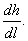 (4.3), (4.4), (4.7), (4.9) в уравнение (4.2) и решая его относительно, получим общий вид уравнения неравномерного движения потока при установке в русле поперечной запани
(4.3), (4.4), (4.7), (4.9) в уравнение (4.2) и решая его относительно, получим общий вид уравнения неравномерного движения потока при установке в русле поперечной запани
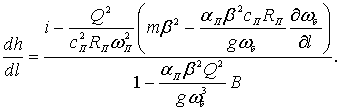 (4.10)
(4.10)
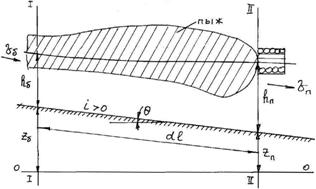
Рисунок 4.5 Расчетная схема для определения величины подпора
В случае установки запани в призматическом русле 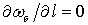 , и тогда уравнение (4.10) преобразуется к виду
, и тогда уравнение (4.10) преобразуется к виду
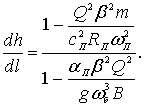 (4.11)
(4.11)
При известных геометрических параметрах русла и пыжа, характе ристиках потока можно составить алгоритм расчета кривой свобод ной поверхности в верхнем бьефе лесозадерживающей запани.
