Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

5.6 Динамика воздействия гидравлической струи на неподвижную преграду

В основу вывода динамических свойств струи положена теорема о количестве движения. Рассмотрим общий случай удара струи о неподвижную преграду.

Пусть в сечении 1-1 (рисунок 5.8) струя имеет площадь живого сечения w и среднюю скорость потока u. При встрече с преградой струя разделится на две части с характеристиками w₁u₁ и w₂u₂. Используя теорему о количестве движения, можно записать

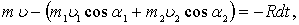  (5.37)

где Rdt – импульс силы, реакция стенки.

Реакция R равна силе удара струи, то есть можно написать – R = F.

Если a₁ = a₂ = 90°, то уравнение (5.37) можно записать

m u = F dt, где m = g/g w u².

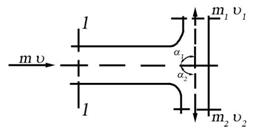
Рисунок 5.8 Схема растекания струи

С учетом значения m из уравнения (5.37) получим выражение для определения силы удара струи о преграду

F = g/g Q u = g/g w u². (5.38)

Разделив уравнение (5.38) на w, полученную величину F/w можно представить как динамическое давление на единицу площади струи. Это давление равно удвоенному скоростному напору.

Статическое давление струи Р_ст = r g w H, где Н – напор над центром тяжести отверстия, из которого истекает струя.

Динамическое давление струи Р_дин = g/g w u² = g/g w 2 g H = 2 g w H, т.е. динамическое давление в 2 раза больше статического.

Если пластина перемещается со скоростью u < u в направлении скорости u, относительная скорость равна (u - u), и тогда сила давления струи на подвижную плoтину равна

F = r Q (u - U) = r w (u - U)²  .  (5.38a)

Если помещенная в струю пластина (диск) имеет ограниченные размеры, то силу давления на неподвижный диск можно определить по формуле [44]

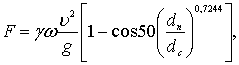  (5.39)

где d_п – диаметр пластины;

 d_с – диаметр струи;

 u – средняя скорость на уровне пластины.

Выражение в квадратных скобках представляет собой корректив, учитывающий соотношение d_п и d_с

При значении 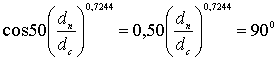 и d_п/d_с = 2,22, следовательно когда d_п > d_с. в 2,22 раза, силу давления на нее можно определить так же, как при набегании струи на неограниченную плоскость.

Исследования Конопкина Б.К. [44] позволяют сделать вывод, что если d_п/d_с изменяется в пределах от 0 до 2,22, то силу давления можно определить по формуле (5.40), если d_n/d_c > 2,2 силу давления можно определять, как при набегании струи на пластину неограниченных размеров.

Силу удара струи можно определить по формуле профессора Никонова Г.Н. [45]

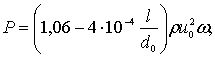
где d₀ – диаметр сопла;

 l – расстояние от среза сопла до рассматриваемого сечения;

 u₀ – выходная скорость потока из сопла;

 w – площадь сопла.

Более сложным представляются процесс изучения динамического воздействия струи на перемещающееся в ней тело.

Определим силу давления затопленной гидравлической струи на пластину (диск), перемещающуюся в возбужденном потоке (рисунок 5.9).

Силу давления струи на плоский диск можно определить, воспользовавшись известной в гидромеханике формулой сопротивления воды движению тел

F = c W r   (5.40)

где с – коэффициент сопротивления;

 u – скорость движения тела или скорость набегающего потока жидкости.

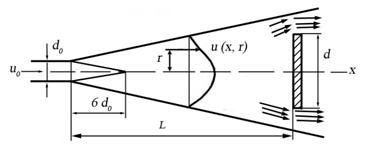
Рисунок 5.9 Схема растекания струи

Для определения скорости в заданной точке сечения возбужденного потока u(x, r), удаленной на расстоянии L от насадка ускорителя, воспользуемся формулой Альбертсона [36, 42]

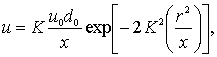  (5.41)

где u₀ – скорость истечения жидкости из насадка ускорителя;

 d₀ – диаметр насадка;

 К – опытный коэффициент, К = 6,4.

Подставляя значение скорости (5.41) в формулу (5.40) для определения силы давления струи на диск диаметром d, расположенном на расстояниих = l от насадка, получим

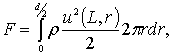
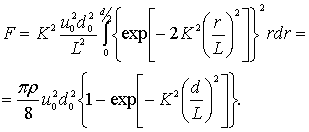  (5.42)

Принимая exp @ 1 + x, формулу (5.42) можно представить следующим образом:

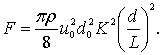  (5.43)

Таким образом, по формулам (5.42) и (5.43) может быть определена сила давления струи на диск, помещенный в возбужденный поток, а по формуле (5.40) величина сопротивления воды движению этого диска.

Зная R и F, можно установить закономерность движения диска в водном потоке, воспользовавшись уравнением движения тела в водном потоке

m du/dt = F – R,

где m du/dt – силы инерции.

С учетом полученных значений F и R запишем

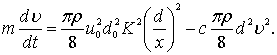
Введем обозначения в это уравнение

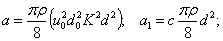
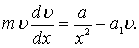 (5.44)

Полученное дифференциальное уравнение движения тела в возбужденном потоке не имеет точного решения. Кроме того, в уравнении (5.44) не учитывается толщина диска, т.е. изменение скорости возбужденного потока вдоль тела (диска).

Воспользовавшись методом численного интегрирования, можно проследить качественную характеристику изучаемого процесса на некоторых частных случаях. На графиках (рисунок 5.10) приведены результаты расчетов по определению скорости движения диска на различном расстоянии от среза насадка.

График 1 показывает, что при достаточном большом расстоянии от насадка скорость тела резко уменьшается с увеличением расстояния, а затем постепенно затухает.

На графике 2 видно, что если начальное расстояние диска от насадка уменьшить (при неизменных остальных параметрах), то наблюдается резкий скачек скорости, а затем плавное убывание, как и в первом случае.

Графики 3 – 8, построенные для различных сочетаний скорости истечения потока из насадка, размеров диска, показывают на наличие прыжка скорости на начальном участке и постепенное плавное ее гашение.

К сожалению, до настоящего времени приведено мало исследований, изучающих закономерности движения лесосплавных единиц в водном потоке, возбужденном затопленной гидравлической струей.

Укажем на исследование профессора В.П. Корпачева [46], в котором приведена приближенная формула для определения скорости движения пучка в сечении, удаленном на расстоянии L  от насадка

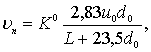  (5.45)

где u_п – скорость движения пучка в рассматриваем сечении, м/с;

 U₀ – скорость потока на выходе из насадка диаметром d₀;

 К⁰ – опытный коэффициент, зависящий от объема пучка и способа его установки относительно оси потока, определяется по графику (рисунок 5.11).

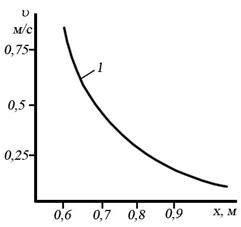
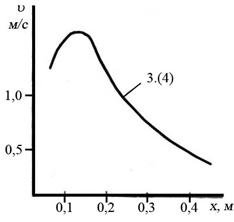
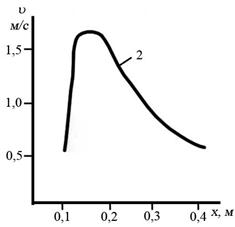
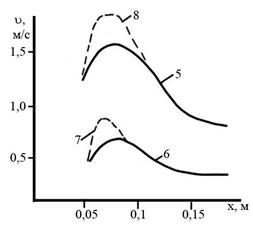
Рисунок 5.10

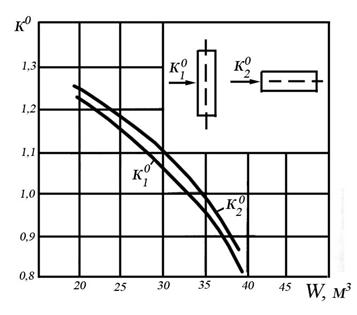
Рисунок 5.11 Значение коэффициента К⁰