Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

6.5 Основные зависимости линейной теории плоских прогрессивных волн в случае ограниченной глубины (Н = const)

В этом параграфе излагаются результаты теоретических исследований без доказательств, так как они аналогичны рассуждениям предыдущего параграфа.

Потенциал скорости прогрессивных волн относительно малой амплитуды, распространяющихся вдоль положительного направления оси x имеет вид

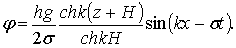  (6.30)

Уравнение волнового профиля запишется

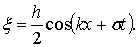  (6.31)

Эта формула аналогична формуле (6.20), определяющей форму профиля волны при Н = ¥, различно лишь значение величины h/2. В формуле (6.31), т.е. при Н = const

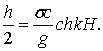 (6.32)

Профиль волны имеет форму косинусоиды с амплитудой h/2. Если принять x = 0 при t = 0 , то форма профиля волны изобразится косинусоидой, представленной на рисунке 6.3, с вершиной на оси z.

С изменением x или t значения cos (k x₀ –σ t) изменяются в пределах от +1 до -1 и x последовательно принимает все значения от x = h/2 (вершина волны) до x = – h/2  (подошва волны). Следовательно, высота волны

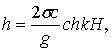
Откуда

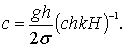  (6.33)

Скорость перемещения профиля волны с вдоль оси х равна:

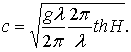  (6.34)

Так как с = λ/z, то связь между периодом и длиной волны запишется

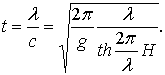  (6.35)

Скорость волны в общем случае зависит как от периода волны, так и от глубины жидкости. Если глубина жидкости велика по сравнению с длиной волны, т.е. 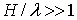 и 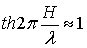, то из выражения

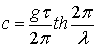
получим известное значение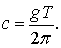 

Если глубина жидкости мала по сравнению с длиной волны (как, например, при распространении приливных волн в морях и океанах), т.е. 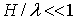 и 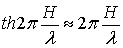, то скорость волн оказывается зависящей только от глубины жидкости:

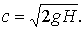
Горизонтальная и вертикальная скорости частиц жидкости, совершающих волновое движение, определяются через потенциал скорости (6.23):

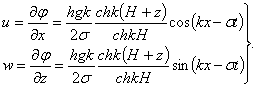  (6.36)

Траектории частиц жидкости, т.е. их координаты определяются по формулам:

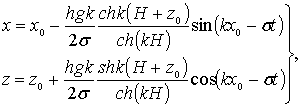  (6.37)

где  x₀, z₀ – координаты, которые имела частица жидкости в невозмущенном состоянии.

Избыточное гидродинамическое давление в волне при Н = const определится из уравнения Лагранжа (6.1), подставляя в него значение производной потенциала скорости j (6.30), т.е.

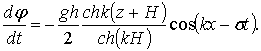  (6.38)

Подставив значение dj/dt в уравнение (6.1), получим величину избыточного давления в точке волны с координатой x

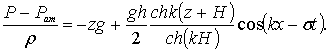  (6.39)

В этом уравнении второе слагаемое правой части представляет волновое давление в точке z.