Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.6 Энергия волн
Ветровые волны являются мощным источником энергии. С одной стороны энергию волн можно рассматривать как дополнительный вид энергии. Это, например, преобразование энергии волн в электрическую энергию (приливные электростанции). Мощность волны на 1 м длины фронта при высоте волны в 1,25 м составляет 75 кВт/м. Мощность волны заметно падает при их приближении к берегам.
И в тоже время силовое воздействие волн на берега, гидротехнические сооружения, лесосплавные объекты вынуждают изыскивать способы гашения энергии волн.
Сущность трансформации волны при подходе к берегам, встрече с каким-либо сопротивлением основывается на уравнении баланса энергии.
Полная энергия одной бегущей волны равна сумме потенциальной и кинетической энергии
E = En + Ek (6.40)
Ранее (6.4.3) отмечалось, что при Н = ¥ гидродинамическое давление,испытываемое частицей жидкости в волнах при спокойномуровне,одинаково. Поэтому потенциальная энергия частицы жидкости обусловлена только лишь своим высотным положением в сравнении с положением той же частицы жидкости при спокойном уровне.
Потенциальная энергия волны может быть определена по формуле
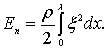(6.41)
Кинетическая энергия равна
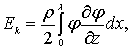(6.42)
где j – потенциал скорости;
x – ординаты кривой свободной поверхности.
Эти уравнения справедливы для всего объема волны от дна до поверхности (Z = 0). Так как ось Z направлена вверх и имеет свое начало на статическом горизонте, то во всех случаях Z < D.
Для волн малой глубины потенциал скорости запишется по формуле (6.30).
Координаты точек профиля волны, т.е. превышение точек свободной поверхности волны над их положением в состоянии покоя определим, дифференцируя потенциал скорости (6.30), т.е.
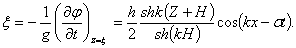(6.43)
Подставляя значения (6.30) и (6.43) в формулу (6.41), (6.42) и интегрируя, получим
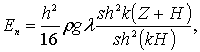(6.44)
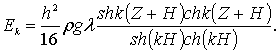(6.45)
Подставляя значения (6.44) и (6.45) в формулу (6.40), получим
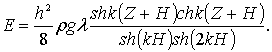(6.46)
Для случая Z = 0 , т.е. для всего объема бегущей волны получим следующее значение полной энергии:
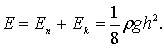(6.47)
Для практических целей представляет интерес закон распределения энергии по глубине Z. Знание этого закона необходимо при конструировании различного типа волногасителей. Закон распределения энергии по глубине получим, дифференцируя выражения (6.44), (6.45),
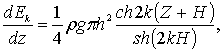(6.48)
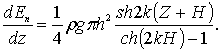(6.49)
Введем следующие обозначения [53]:
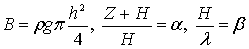. (6.50)
Величина В не влияет на закон распределения энергии по вертикали, т.к. зависит только от высоты волны.
Величина a - это превышение точки над дном, выраженное в долях полной глубины. Для дна a = 0, для поверхности a = 1. Величина bопределяет закон распределения энергии по глубине является основной характеристикой волнового режима. С учетом принятых обозначений получим:
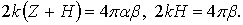(6.51)
Подставляя значения (6.51) в формулы (6.48) и (6.49), получим закономерность распределения энергии по глубине с учетом принятыхобозначений, т.е.
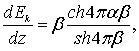(6.52)
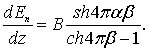(6.53)
Ведем функции y1, y2 = f (a, b)
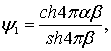
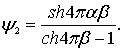
С учетом принятых значений функций y1 и y2, выражения (6.52) и (6.53) запишутся [52]:
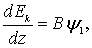
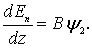
Принимая значения b от b = 0,1 до b = 1,0, можно подсчитать значения y1 = f (a) и y2 = f (a) и построить графики (рисунок 6.4).
Графики показывают, что с уменьшением относительной глубины кинетическая энергия распределяется равномерно по глубине.
Распределение энергии волны по глубине можно определить, анализируя формулу
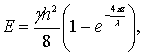(6.54)
где z - глубина слоя, для которой определяется волновая энергия, отсчитьгваемая от свободной поверхности жидкости.
На рисунке 6.5 построен график E = f(z).
При глубине l/h = 10 (кривая 1) в слое глубиной Z = 4 h или Z = 0,4l сосредоточено почти 99 % волновой энергии, а при l/h = 20 (кривая 2) то же количество энергии сосредоточено в слое глубиной Z = 8h или Z = 0,4l. При Z = 0,52l,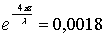 
, т.е. в пределах границы ограниченной глубины энергии волны E0,5l = 0,998 Е.
Одним из энергетических показателей волнового движения является поток энергии, который возникает при любой степени волнения. На поверхности воды, как правило, формируются волны разных периодов с различными скоростями распространения. Накладываясь друг на друга, они образуют группы волн, распространяющиеся со скоростью, отличной от скорости отдельных волн. Так называемая групповая скорость является чисто кинематической волновой характе ристикой, так как описывает скорость распространения группы волн. Однако она имеет важную динамическую роль – с групповой скоростью происходит перенос энергии волн.
Усредненный за период волны поток энергии Э, проходящий через сечение единичной ширины и высоты Н, расположенное вдоль фронта волны, определим интегрированием по времени:
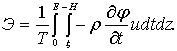(6.55)
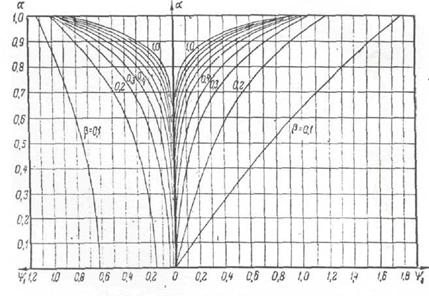
Рисунок 6.4 График зависимости y1, y2 = f (a, b)
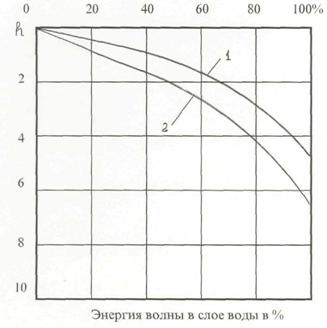
Рисунок 6.5 Распределение энергии волны по глубине
Используя выражение для потенциала скорости (6.30) и интегрируя (6.55), получим:
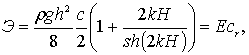
где сr - групповая скорость
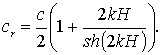(6.56)
При Н ® ¥ групповая скорость равна 0,5 С. С переходом на мелководье групповая скорость возрастает, однако никогда не достигнет скорости распространения волны, так как разрушение волны наступит раньше.
Механизм переноса волновой энергии заключается в переносе частицами воды связанных с ними количеств энергии. Здесь необходимо отметить, что частица жидкости пересекает некоторую вертикальную плоскость, перпендикулярную к направлению распространения волны, дважды - в направлении распространения волны и двигаясь в обратном направлении. Перенос энергии носит пульсирующий характер. При этом количество кинетической энергии, переносимой в сторону распространения волны, равно количеству кинетической энергии, переносимой волной в обратном направлении (при Н ® ¥). Кинетическая энергия остается таким образом привязанной к месту и лишь участвует в пульсации волновой энергии. Потенциальная энергия перемещается в сторону распространения волны. Из формул (6.44) и (6.45) следует, что количество кинетической и потенциальной энергии, заключенное в полном объеме волны, равно между собой.
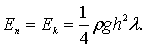(6.57)
При движении волны на конечной глубине (Н = const) в сторону распространения волны переносится не только потенциальная, но частично и кинетическая энергия.