Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

6.2.1 Линейная и нелинейная теории волн

Теоретические и экспериментальные исследования в области волнового движения настолько трудны, что до сих пор нет единой удовлетворительной полной теории волн.

Волновые процессы описываются в общем случае двумя теориями - линейной и нелинейной.

Линейная теория построена на двух предположениях:

1) малость величины, т.е n, изучаемые поверхностные волны достаточно пологи, крутизна их мала;

2) волновое движение жидкости происходит достаточно медленно, скорости движения частиц жидкости настолько малы, что их квадратами и высших степеней можно пренебречь.

Решение задачи движения волн с учетом нелинейности условий рассматривается в нелинейной теории волн. Точные решения с учетомнелинейности граничных условий на свободной поверхности жидкости очень сложны.

Для практических расчетов используют приближенные решения, где, как правило, за первое приближение принимается решение по линейной теории.

Линейная теория применима для так называемых волн малой амплитуды, определение которых следует из двух вышеназванных предположений этой теории.

Нелинейная теория применима к волнам большой высоты.

«Волнами большой высоты называются волны, не удовлетворяющие определению волн малой высоты, т.е. волны, высота h которых настолько велика в сравнении с их длиной λ, что частицы жидкости в волне движутся с такой большой скоростью υ, что в математических выражениях теории волн нельзя пренебречь величиной υ², а также произведениями скорости υ на малые величины» [47]. Полной математической теории волн большой высоты пока не разработано, хотя разработке теории волн большой высоты исследователи уделили большое внимание - Герстнер, Ренкин, Релей, Стокс, Буссинеск, Миша и др.

Недостаток существующих теорий волн большой высоты заключается в том, что каждая из них пригодна лишь в ограниченном диапазоне параметров волн.

Между волнами малой и большой высоты, соответственно линейной и нелинейной теорией, нет четкого числового разграничения, хотя в работе [51] указывается, что таким критерием может служить число URSELL.

Если число URSELL 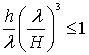 при h/H £ 1, то приемлема линейная теория для волн малой высоты.

Для нелинейной теории параметр URSELL зависит от относительной высоты волн:

при h/H £ 1, число URSELL < 10;

при h/H < 1, число URSELL = 1;

при h/H <  > 1, число URSELL >> 1.

Анализ раннее выполненных исследований дает возможность установить область применения линейной и нелинейной теории волн.

Линейная теория применима:

1) для расчета гравитационных сооружений, когда доминирующей составляющей волновой нагрузки является инерционная;

2) для расчета волновых воздействий на элементы сооружений (за исключением тонких элементов) [45];

3) для определения волновых нагрузок на заякоренные объекты[49], плавучие волноломы [50].

Нелинейную теорию можно применять:

1) при определении сопротивления движению тела на волнении;

2) исследования взаимодействия плавающего  объекта при его качке [50];

3) при исследовании или расчете влияния скоростной составляющей волновой нагрузки [48].