
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.4.1 Уравнение волнового профиля
Основные параметры линейных волн могут быть получены из выражения потенциала скорости (6.16) и уравнения Лагранжа (6.1). В формуле потенциала скорости, записанного в виде (6.16), для случая глубокой воды, т.е. при 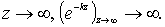
Величина 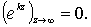
Очевидно, что предположение о неограниченном возрастании с глубиной значения 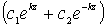 , а следовательно, и потенциала скоростей не имеет физического смысла. Поэтому постоянную можно принять равной нулю. Тогда, принимая значение c1 = c, из уравнения (6.16) получим
, а следовательно, и потенциала скоростей не имеет физического смысла. Поэтому постоянную можно принять равной нулю. Тогда, принимая значение c1 = c, из уравнения (6.16) получим
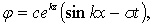 (6.17)
(6.17)
т.е. потенциал скорости экспоненциально убывает с глубиной.
Уравнение волнового профиля определится из условий равенства давлений P = Pат для точек свободной поверхности. В этом случае уравнение (6.1) примет вид (при z = x)
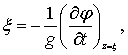 (6.18)
(6.18)
где x – координата точек линии свободной поверхности.
Уравнение волнового профиля получим из уравнения (6.4), подставляя в него значение производной потенциала скорости,
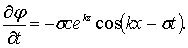 (6.19)
(6.19)
С учетом граничных условий Z = Z0 = 0 и x = x0, получим
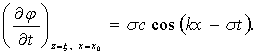
Подставляя это выражение в (6.18), получим
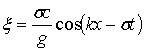
или с учетом значения c = gh/2σ, получим
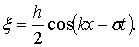 (6.20)
(6.20)
Профиль волны имеет форму косинусоиды с амплитудой h/2. С изменением х или t значение cos(k x – σ t) изменяется в пределах от 1 до-1 и xпоследовательно принимает все значения x = h/2 (вершины волны) до x = - h/2 (подошвы волны) (рисунок 6.3).
При t =const значения cos(k x – σ t) одинаковы для точек профиля волны, абсциссы x которых разнятся на 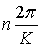 , где n – целое число. Разность абсцисс точек при n = 1 равна длине волны λ. Поэтому
, где n – целое число. Разность абсцисс точек при n = 1 равна длине волны λ. Поэтому
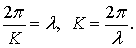
Для любого определенного x =const значение cos(k x – σ t) повторяются в моменты, для которых t разнятся на величину 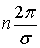 , где n – целое число. Промежуток времени между такими моментами при n = 1 равен периоду волны τ. Поэтому
, где n – целое число. Промежуток времени между такими моментами при n = 1 равен периоду волны τ. Поэтому
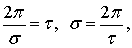
где σ – угловая скорость.
Волна, сохраняя свою форму, перемещается вдоль положительной оси x с постоянной скоростью c
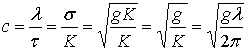 (6.21)
(6.21)
или при g = 9,8 м/с, 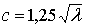 м/с.
м/с.
Период волны
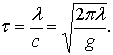 (6.22)
(6.22)
Из формулы (6.21) и (6.22) видно, что c и τ зависят только от длины волны.
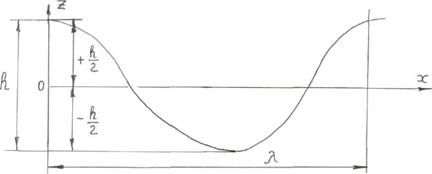
Рисунок 6.3 Форма профиля волны при х = 0, t = 0, построенного по формуле (6.19)
