Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.4.2 Скорость движения частиц жидкости в волне
Рассмотрим движение отдельных частиц жидкости в волне. Проекции скорости движения частицы жидкости на оси координат выражаются через потенциал j:
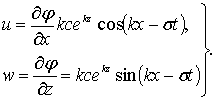(6.23)
Подставляя в эти формулы значения k = σ2/g и с = gh/σ, получим
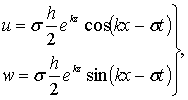(6.24)
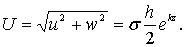(6.25)
Из формулы (6.25) видно, что скорость движения частиц жидкости в гребне волны несколько больше скорости во впадине. Однако в волне малой высоты координаты z частицы изменяются незначительно, поэтому скорость движения частицы на ее траектории почти постоянна. Поэтому при z = z0можно записать
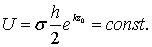(6.26)
Формулы (6.25) и (6.26) показывают, что скорость U убывает вниз и равна нулю при z = - ¥.
Uz=-¥ = 0,
следовательно, на дне, где z = - ¥, частицы жидкости находятся в состоянии покоя.
Положение частицы жидкости в волне определяется координатами
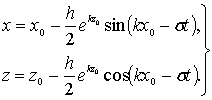(6.27)
где x, z – координаты частиц жидкости в волне.
Уравнение траектории частицы жидкости в волне может быть записано в виде уравнения окружности
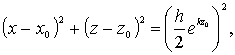
т.е. в волнах частицы жидкости движутся по замкнутым орбитам, имеющим форму окружностей с радиусами, быстроубывающими по вертикали вниз
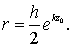
На свободной поверхности жидкости, где z0 = 0, rпов = h/2, на глубине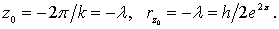 
На дне, где z0 = – ¥, 
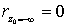, т.е. частицы жидкости находятся в состоянии покоя.