Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.7.5 Определение волновой нагрузки на движущийся лесосплавной объект
Сила волновой нагрузки на движущееся в потоке тело может быть определена по формуле (6.69), подставив в нее значение силы давления на носовую поверхность Р1 (6.75) и кормовую поверхность Р2 (6.77) с учетом значений изменившихся параметров волн. Эти изменения параметров волн вызваны тем, что при движении тела в условиях волнения время встречи с вершинами двух последующих волн будет отличаться от истинного значения периода τ.
Соответственно длина волны и скорость ее распространения принимают другие значения, назовем их кажущимися или фиктивными. Введем обозначения:
τф – фиктивный период волны;
lф – фиктивная длина волны;
Cф – фиктивная скорость распространения волны;
Kф – фиктивное волновое число;
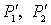– сила волнового давления на носовую и кормовую поверхности движущейся лесотранспортной единицы;
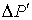– сила суммарного волнового давления на подвижную лесотранспортную единицу.
С учетом принятых значений формулы (6.75), (6.77) и (6.78) примут вид:
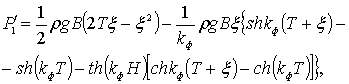(6.79)
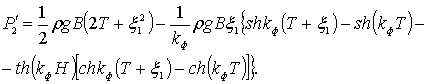(6.80)
Сила волнового давления на подвижную лесотранспортную единицу определится по формуле
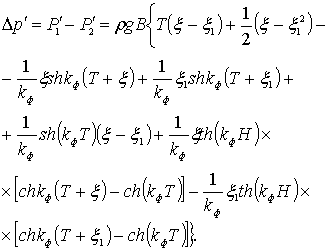(6.81)
Определим, входящие в формулы (6.79), (6.80), (6.81), значения параметров волн взаимодействующих с движущейся лесотранспортнои единицей.
Между параметрами волн τф, lф, Cф, Kф существует определенная взаимосвязь. В формулах (6.79-6.81) необходимо установить значение фиктивного волнового числа Kф, то есть значение параметра, учитывающего изменение величины волнового числа при взаимодействии волны с движущейся лесотранспортнои единицей.
В общем случае период волны τ = l/c.
При движении тела на взволнованной поверхности
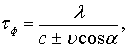(6.82)
где u – скорость движения лесотранспортнои единицы;
a – угол между курсом лесотранспортнои единицы и направлением бега волны.
В знаменателе формулы (6.82) при встречном движении тела и волны принимается знак плюс, при попутном – минус. Если a = 0, то формула (6.82) запишется
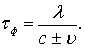(6.83)
Определим фиктивную скорость распространения волны и фиктивную длину волны.
Скорость распространения волны для водоемов с глубокой и малой глубиной определится по формуле
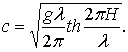(6.84)
Для кажущейся фиктивной глубины волны lф фиктивная скорость распространения запишется
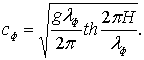(6.85)
Фиктивный период волны определится
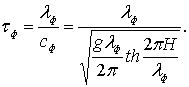(6.86)
Приравнивая правые части уравнений (6.83) и (6.86) и подставляя значение скорости С из формулы (6.83), получим
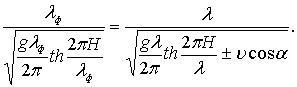(6.87)
Равенство (6.87) может быть решено для интересующих нас практических случаев.
Определим lф и Кф для случая глубокой и малой глубины при встречном движении α= 0 (α - угол между курсом тела и направлением бега волны):
1) a = 0, глубокая волна, то есть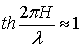 
.
Для принятых условий из формулы (6.87) получим значение
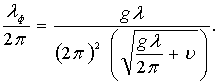(6.88)
Левая часть выражения (6.88) представляет величину, обратно пропорциональную волновому числу Кф, поэтому, подставив в формулу (6.88) значение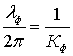 
, можно определить фиктивное волновое число
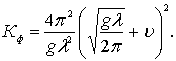(6.89)
2) a = 0, малая глубина l > 2Н.
В этом случае максимальная граничная глубина Н = 0,5l. Принимая l = a lф,, где а – коэффициент, связывающий истинную длину волны и фиктивную (Н = 0,5 a lф), из формулы (6.87) получим
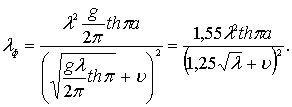(6.90)
Выразим из формулы (6.90) фиктивное волновое число, учитывая, что
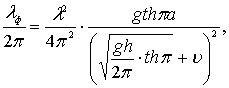
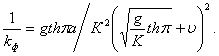(6.91)
Таким образом, зная значение Кф, можно определить суммарное волновое давление как на глубокой, так и на мелкой воде в случае движения лесотранспортной единицы навстречу волне.