Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.2.1 Сопротивление трения
При рассмотрении движения твердого тела в жидкости удобно весь объем разделить на три области. Первая находится в непосредственной близости к поверхности тела, где в наибольшей степени проявляются силы вязкости, и называется пограничным слоем. Сходящий с тела пограничный слой образует вторую область, попутную струю или попутный поток. Вся остальная масса жидкости вне пограничного слоя и попутной струи составляет третью область – потенциальный поток.
Сопротивление трения представляет проекцию результирующей всех элементарных касательных сил, действующих вдоль смоченной поверхности судна или лесотранспортной единицы на направление движения. Сопротивление трения является результатом действия сил вязкости воды, которые возникают в пограничном слое воды, примыкающем к поверхности корпуса тела.
Влияние сил вязкости проявляются только лишь в пределах пограничного слоя. В зоне внешнего потока влияние этих сил ничтожно и его можно рассматривать потенциальным течением жидкости. Толщина пограничного слоя относительно мала по сравнению с длиной тела и принимается равной расстоянию от стенки тела до границы потока, на которой скорости частиц жидкости составляют 0,995 скорости потенциального потока. Особенность пограничного слоя заключается в том, что давление по его сечению постоянно, т.е. пограничный слой передает давление на поверхность тела таким же, как на поверхности раздела потока на зону пограничного слоя и внешнего потенциального потока.
Внутри пограничного слоя скорость частиц жидкости резко изменяется от нуля на поверхности тела до скорости потенциального потока на внешней границе пограничного слоя. Такое резкое изменение скорости при сравнительно малой толщине пограничного слоя и обуславливает проявления в нем сил вязкости жидкости. Пограничный слой либо плавно сходит с задней кромки тела, либо срывается с его поверхности, в обоих случаях образуя за телом так называемый след или попутную струю, т.е. пограничный слой является источником вихреобразования за движущимся телом.
Внутри пограничного слоя может наблюдаться ламинарный или турбулентный режим течения. Для определения критического числа Рейнольдса за характерный линейный размер принимается толщина пограничного слоя d, т.е.
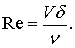(7.15)
Каждому режиму течения соответствуют свои законы распределения скоростей и касательных напряжений.
Первые опыты по определению сопротивления трения досок были предприняты еще во второй половине XYIII века. Однако более надежные результаты были получены в семидесятых годах прошлого столетия Фрудом. Он проводил буксировочные испытания полностью погруженными досками различной длины и с различной степенью шероховатости. При полном погружении сопротивление формы и волновое сопротивление равно сопротивлению трения. Фрудом была предложена эмпирическая формула
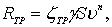(7.16)
где g – объемный вес воды;
z – коэффициент трения, зависящий от длины доски и степени шероховатости поверхности;
S – смоченная поверхность доски;
υ – скорость движения доски;
n – показатель степени зависящий от шероховатости поверхности; n = (1,8–2,0).
Эта формула путем экстраполяции экспериментальных данных была перенесена и для вычисления сопротивления трения судов, причем показатель степени n принимается равным 1,825. Формула Фруда долгие годы использовалась в судостроении для определения Rтр.
Более поздние исследования показали, что расчеты сопротивления трения по формуле Фруда дают заниженные результаты.
Результаты многолетних исследований показали, что величина сопротивления трения зависит от скорости движения тела, от размеров и степени шероховатости подводной части тела, а также от физических свойств жидкости – ее плотности и вязкости; на сопротивление трения большое влияние оказывает режим движения жидкости внутри пограничного слоя вдоль поверхности тела.
Теоретический расчет сил трения с одновременным учетом всех действующих факторов представляет большие трудности, наиболее полно определено лишь сопротивление трения для тел простейшей формы – плоской технически гладкой пластины, движущейся в направ лении своей плоскости. Поэтому расчет сил трения трехмерных тел ведется по упрощенной схеме.
Сопротивление трения при этом можно определить двумя способами:
1) непосредственно интегрированием по смоченной поверхности касательных напряжений, полученных теоретическим или экспериментальным путем;
2) расчетом по общей формуле:
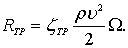(7.17)
В этой формуле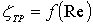 
определяют, используя некоторые допущения.
Первое допущение сводится к тому, что сопротивление трения корпуса судна или лесотранспортной единицы рассчитывается как сопротивление трения эквивалентной технически гладкой пластины.
Технически гладкой поверхностью принято считать поверхность, неровности которой (бугорки, шероховатости) практически не оказывают влияния на сопротивление движению тела.
Второе допущение заключается в том, что влияние шероховатости поверхности судна или лесотранспортной единицы учитывается отдельно, введением так называемых надбавок на шероховатость и кривизну корпуса.
Так, сопротивление трения Rтр судна определяется по формуле [62, 65]
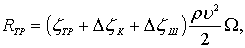(7.18)
где zтр – коэффициент сопротивления трения технически гладкой эквивалентной пластины при турбулентном обтекании;
DzК, DzШ – надбавки к коэффициенту сопротивления трения за счет кривизны и шероховатости судовой поверхности;
W – площадь смоченной поверхности судна, определяемая по теоретическому чертежу судна или по формуле
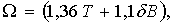(7.19)
d – коэффициент полноты водоизмещения судна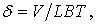 
L, B, T – главные размерения судна;
V – объем подводной части судна.
Для определения коэффициента сопротивления трения имеется ряд формул. Наибольшее распространение как в отечественной, так и в зарубежной практике получила формула Прандтля – Шлихтинга
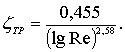(7.20)
Подобное решение задачи по определению коэффициента при различных режимах обтекания пластин и его численные значения приведены в главе 7.3.
Значения поправок на кривизну DzК при числе Фруда Fr £ 0,35 могут быть определены по эмпирической формуле Хорна
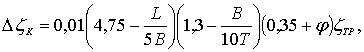(7.21)
где j – коэффициент продольной полноты судна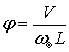 
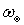– площадь мидель–шпангоута.
В практике при пересчете результатов испытания модели на натуру полагают DzК = 0 , относя увеличение сопротивления трения за счет привязки к остаточному сопротивлению, определяемому из опыта над моделью.
Величина DzШ зависит от многих факторов, и её точное значение для данного судна и случая определяется по результатам испытаний. В качестве средних могут быть приняты следующие значения DzШ
Тип судна
Суда сварные:
- быстроходные................................ (0,3 – 0,5) ×10–3;
- транспортные и пассажирские со средними и низкими относительными скоростями.............................................. (0,4 – 0,6) ×10–3;
Суда клепаные и сварные со значительной волнистой
поверхностью............................................ (0,65 – 1.0) ×10–3.