Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

7.3.1 Теоретическое решение задачи о трении потока вдоль пластины при ламинарном обтекании

Установление физической картины обтекания пластины водным потоком и определение величины сопротивления воды движению пластины представляет практический интерес, поскольку, во–первых, по сопротивлению трения технически гладкой пластины рассчитывается сопротивление трения судов, плотов, лесотранспортных единиц; во–вторых, на лесосплаве обтекание лесонаправляющих, лесозадерживающих сооружений, рейдовых наплавных сооружений, отдельных узлов сплоточных и формировочных машин несколько подобно обтеканию плоских пластин.

Величина сопротивления трения может быть определена аналитическим путем, и в то же время результаты такого решения наиболее полно поддаются экспериментальной проверке, поскольку сопротивление трения плоской пластины является полным ее сопротивлением.

Рассмотрим расчет сопротивления пластины при ее ламинарном обтекании. Для аналитического исследования движения жидкости в пограничном слое при обтекании пластины установившимся ламинарным потоком могут быть использованы дифференциальные уравнения движения вязкой жидкости Навье–Стокса, записанные в следующем виде:

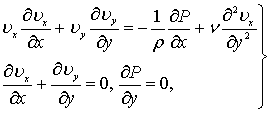 (7.31)

где   х – абсцисса, отсчитываемая вдоль поверхности тела;

у – ордината по нормали к поверхности тела.

Эта система уравнений называется уравнениями Прандтля для пограничного слоя (ламинарного).

В уравнениях (7.31) u_x, u_y – неизвестные функции от X, Y; Р – известная функция от X, которая определяется по значениям давления потенциального потока в точках внешней границы пограничного слоя. Для интегрирования уравнений (7.31) введем функцию тока y,удовлетворяющую уравнению неразрывности, т.е. второму уравнению системы (7.31). Тогда компоненты скорости u_x, и u_y через функцию тока yопределяются по формулам:

, 

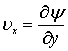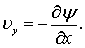
С учетом этих выражений первое уравнение системы (7.31) запишем в таком виде:

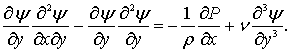  (7.32)

Поскольку градиент давления в направлении нормали к стенке 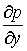 очень мал по сравнению с величиной 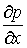, то изменение в поперечном направлении пограничного слоя можно с достаточной степенью точности не учитывать и принимать давление по толщине слоя практически постоянным и равным давлению на его внешней границе, следовательно, .

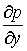Для плоской пластины продольный перепад давления 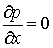, поэтому уравнение (7.32) принимает вид:

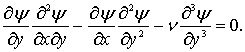  (7.33)

При решении задачи следует учитывать граничные условия, согласно которым на поверхности пластины наблюдается прилипание частиц жидкости, т.е. u_x = u_y = 0, и следовательно, y = 0,

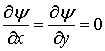 при y = 0, x > 0.

На бесконечном удалении от пластины скорость стремится к скорости набегающего потока, т.е. u_x ® u и следовательно, y = 0,

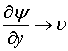 при у ® ¥.

Для решения уравнения (7.33) введем безразмерные характеристики. Параметры потока около пластины зависят от координат х и у, скорости u и вязкости жидкости n. Безразмерные координаты x, z, определяемые названными характерными величинами, имеют вид [63]

, .

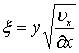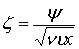С помощью введенных переменных x, z Блазиусу удалось преобразовать исходное уравнение (7.33) к следующему виду

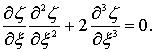  (7.34)

При интегрировании этого уравнения обычные граничные условия, согласно которым при у = 0 компоненты u_х = 0 и u_у = 0 и при u = ¥ скоростьu_х = u, переходят в такие условия, когда при x = 0 переменная z и ее первая производная по x становятся равными нулю, а при z = ¥ первая производная от z по x равной единице.

В результате интегрирования уравнения (7.34) может быть получена зависимость u_х =f(y), по которой из формулы

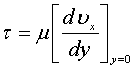
можно определить касательное напряжение непосредственно у поверхности пластины

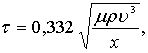  (7.35)

где  m и r – коэффициент вязкости и плотности жидкости;

 u – скорость внешнего потока, которая для плоской пластины постоянна по ее длине;

 x – расстояние от носовой части пластины.

Полное сопротивление пластины длиной l и шириной b, омываемой потоком с обеих сторон, вычислим по формуле:

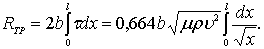
Откуда после интегрирования получим сопротивление трения пластины, обтекаемой ламинарным потоком

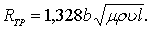  (7.36)

Величину сопротивления трения можно представить по аналогии с формулой (7.16) в виде

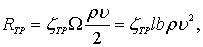  (7.37)

где коэффициент сопротивления трения при ламинарном обтекании будет равен

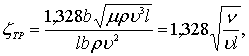  (7.38)

но так как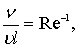  

окончательно имеем

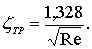  (7.39)

Значения коэффициентов сопротивления трения, рассчитанные по этой формуле, соответствуют результатам опытов с тонкими пластинами при числах Рейнольдса (3 – 5,0)×10⁵, и в этих случаях формулу можно использовать при технических расчетах.