Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

7.3.2 Сопротивление трения плоских пластин при турбулентном обтекании

Решение задачи определения сопротивления трения при турбулентном обтекании пластины представляет большие трудности. Поэтому все методы расчета турбулентного обтекания пластин являются теоретико–экспериментальными и в большинстве основаны на использовании интегрального соотношения для пограничного слоя [64]:

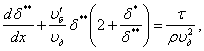  (7.40)

где  d^* – толщина вытеснения, характеризует отклонение линий тока внешнего потока, вызванное влиянием вязкости, по сравнению с направлением линий тока при обтекании тела невязкой жидкостью;

 d^** – толщина потери импульса, характеризует потерю количества движения, связанную с преодолением сил трения жидкости внутри пограничного слоя;

 u_д(x) – характеризует закон изменения скорости потенциального потока вдоль внешней границы пограничного слоя:

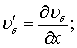
 t – касательное напряжение на стенке.

В уравнении (7.40) неизвестными являются три величины: d^*, отношение d^*/d_u^** напряжение трения

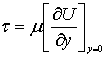
или коэффициент трения z_тр.

В случае турбулентного обтекания пластин величины t и z_тр не могут быть определены непосредственным дифференцированием профиля осредненных скоростей, для этого необходимо задать эмпирический закон сопротивления. Для плоской пластины отсутствует продольный перепад давления, поэтому уравнение (7.40) принимает вид

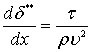
или, введя рейнольдсовые числа

, ,

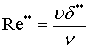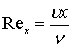получим

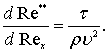  (7.41)

Для установления связи между числом Рейнольдса Re^** и t можно использовать логарифмический закон распределения скорости установившегося турбулентного движения жидкости в трубе,и тогда в результате интегрирования (7.41) может быть получена зависимость для определения коэффициента трения [74]

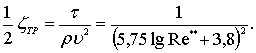  (7.42)

Эта полуэмпирическая зависимость сложна для практического использования. Она обычно заменяется близкой к ней эмпирической.

На основе обработки большого числа экспериментальных данных над длинными пластинами при больших числах Re. получен простой эмпирический степенной закон сопротивления в виде [74]

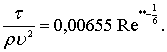  (7.43)

Подставляя в уравнение (7.41) значение (7.43), получим:

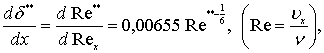  (7.44)

интегрируя (7.44), получим

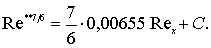  (7.45)

Предполагая, что турбулентный слой устанавливается прямо с передней кромки пластины, т.е. ламинарный участок пренебрежимо мал, тогдаd^** = 0 при х = 0 или, что все равно, Re^** =0 при Re_x = 0. При этих условиях С = 0, и тогда зависимость (7.45) примет вид

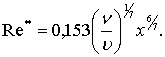  (7.46)

Определив Re^** по формулам (7.45 и 7.46), найдем значение так называемого местного коэффициента сопротивления z_тр.м:

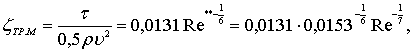
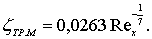  (7.47)

Отсюда уже легко определить полный коэффициент сопротивления пластины длиной l

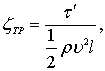
имеем

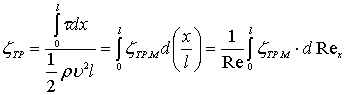
и в силу (7.47)

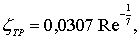  (7.48)

где под Re понимается число Рейнольдса при обтекании пластины, Re = ul/n.

Предлагаемая степенная формула для определения коэффициента сопротивления трения пластины при турбулентном обтекании (7.48) в широком диапазоне чисел Рейнольдса практически не отличается от логарифмической формулы Прандля–Шлихтинга [62]

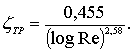  (7.49)

Зависимость (7.49) справедлива для чисто турбулентного обтекания пластины без ламинарного участка в носовой части.

В случае обтекания пластины потоком с различными режимами течения по длине, т.е. смешанным ламинарно–турбулентным потоком, коэффициент сопротивления трения определяется по зависимости [62]:

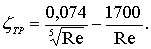  (7.50)

Эта формула предложена Прандтлем и может быть использована при определении коэффициента сопротивления трения пластины в переходной области при числах Рейнольдса, лежащих примерно в пределах Re = (5×10⁵ ¸ 5×10⁶).

Международная конференция опытовых бассейнов (Мадрид, 1975 г.) рекомендует определять коэффициент сопротивления трения по формуле:

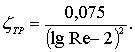  (7.51)