
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.3.3 Сопротивление воды движению пластин при нормальном расположении к направлению потока
Установление физической картины обтекания пластины водным потоком и определение величины сопротивления воды движению пластины представляет практический интерес, поскольку на лесосплаве обтекание лесонаправляющих, лесозадерживающих сооружений рейдовых наплавных сооружений, отдельных узлов сплоточных и формировочных машин подобно обтеканию плоских пластин.
Изучению сопротивления воды движению пластины, расположенной нормально направлению потока, уделено достаточно большое внимание. Этот вопрос рассматривается в большой серии теоретических и экспериментальных работ. Рассмотрим лишь некоторые из них.
Представим неподвижную пластину АВ (рисунок 7.4), помещенную в однородном прямолинейном потоке, скорость U которого нормальна к пластине.
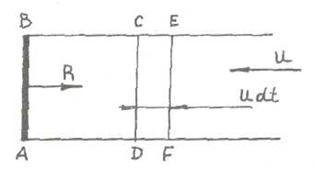
Рисунок 7.4 Сопротивление пластины набегающему потоку
Согласно теории Ньютона, каждая частица жидкости объема Q, ограниченного пластиной АВ и образующими вдоль контура пластины параллельными скорости U, сохраняет величину и направление скорости до момента встречи с пластиной. При ударе о пластину частица теряет свою скорость, следовательно, количество движения Dm–U (Dm – масса частицы жидкости).
В результате потерянного количества движения соответствующая точка пластины получит равный ему импульс. Сумма этих импульсов по всей площади пластины и составит полную величину импульса сил давления потока на пластину.
Обозначим через S площадь пластины, R – давление потока на нее. Пусть через время dt частицы жидкости объема CDEF достигнут поверхности пластины АВ. Тогда сумма потерянного количества движения составит USDm, где SDm – масса объема CDEF, т.е.
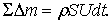
Из теоремы механики о количестве движения получим:
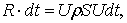
откуда
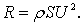 (7.52)
(7.52)
Как показали позднейшие исследования, предположение Ньютона о потере скорости частицами жидкости при достижении пластины не отвечало действительности, хотя качественную зависимость сопротивления от плотности жидкости, площади поперечного сечения и квадрата скорости подтверждают многочисленные классические опыты.
В последующем теоретические и экспериментальные исследования показали, что по мере приближения частиц жидкости к телу они не теряют скорости, а обтекают преграду, создавая вихреобразование перед носовой и за кормовой частями тела.
Многочисленные экспериментальные исследования сопротивления пластин установили следующий общий вид формулы для сопротивления пластины
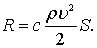 (7.53)
(7.53)
Коэффициент сопротивления при расположении пластины нормально к потоку без ограничения потока по ширине и глубине принимается на основании опытов равным С = (1,1 – 1,15) одинаково для квадратной и круглой пластины и практически не зависит от числа Рейнольдса.
Для прямоугольных пластин величина коэффициета сопротивле ния зависит от соотношения размеров сторон b/l прямоугольника. Чем больше периметр пластины при заданной величине ее площади, тем выше значение коэффициента сопротивления. На рисунке 7.5 приведено графическое изображение зависимости коэффициента С от отношения длины короткой стороны b прямоугольника к длинной стороне l.
Коэффициент сопротивления определен экспериментально для числа Рейнольдса в пределах от 6×103 до 6×105.
Практический интерес представляет величина сопротивления системы двух тонких пластин, расположенных одна позади другой на расстоянии a. Обозначим суммарный коэффициент двух изолированных пластин через 2С и С0 – коэффициент сопротивления одной такой же пластины.
Представим графически (рисунок 7.6) зависимость отношения 2С/С0 для двух круглых пластин от относительного расстояния между ними. При расстоянии между пластинами, равном 1,25d, суммарное сопротивление двух пластин меньше сопротивления одной. При увеличении а/d сопротивление растет и, начиная с 5,0d, взаимное влияние пластин прекращается.
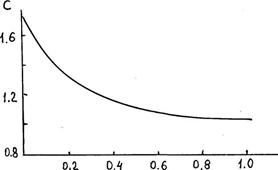
Рисунок 7.5 Зависимость коэффициента сопротивления 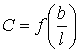
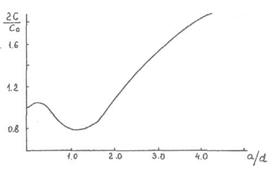
Рисунок 7.6 Зависимость относительного сопротивления 2С/С0 для двух круглых пластин от величины относительного расстояния между ними
Описанное явление частично объясняется экранирующим действием первой пластины на вторую. Опыты Эйффеля показали, что кроме экранирующего влияния, на величину суммарного сопротивления оказывает влияние перераспределение давления между пластинами (таблица 7.1).
Таблица 7.1
| Относительное сопротивление при а/d | |||||||
| 0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | |
| Передней пластины | 1,0 | 1,11 | 1,10 | 1,11 | 1,11 | 1,09 | 1,06 |
| Задней пластины | – | 0,14 | –0,28 | –0,38 | –0,15 | 0,11 | 0,34 |
| Суммарное двух пластин | 1,0 | 0,97 | 0,84 | 0,73 | 0,96 | 1,20 | 1,40 |
Благодаря разряжению за первой пластиной, сопротивление пластины до значений а/d = 2,3 является отрицательным, т.е. давление на заднюю сторону второй пластины на этом расстоянии больше, чем давление на переднюю сторону этой пластины.
Таким образом, сопротивление воды движению одной пластины, расположенной нормально направлению неограниченного потока, может быть определено по формуле (7.53), коэффициент сопротивления при этом принимается равным С = (1,1 – 1,15); коэффициент сопротивления системы двух пластин Сс определяется по графику (рисунок 7.6).
