Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.5.1 Сопротивление воды движению бревен
Как и при обтекании круговых цилиндров, в общем балансе сопротивления одиночного бревна, расположенного поперек потока, преобладает сопротивление формы, которое может быть определено по одночленной формуле
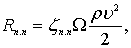(7.55)
где Rп.п – сопротивление одиночного бревна, расположенного поперек потока;
zп.п – безразмерный коэффициент сопротивления этого бревна.
Многочисленные эксперименты показали, что величина сопротивления зависит от числа Рейнольдса и относительной шероховатости. Характеристикой шероховатости служит отношение размеров выступов D к диаметру бревна, т.е. так называемая относительная ше роховатость.
В диапазоне изменения диаметров бревен от 0,1 до 0,6 м и скоростей движения от 0,1 м/с до 0,8 м/с числа Re изменяются сответственно от 104 до 4,8×105, т.е. происходит турбулентное обтекание бревна. В этих пределах величина коэффициента сопротивления постоянна и не зависит от числа Re.
Результаты исследований подтвердили влияние относительной шероховатости на увеличение коэффициента сопротивления одиночного бревна, расположенного поперек потока; на основании опытных данных zп.п – (0,88 – 0,98), тогда сопротивление движению одиночного бревна определится по формуле:
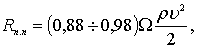(7.56)
где u – скорость движения бревна относительно воды;
W – площадь погруженной части поперечного сечения бревна, определяемая по формуле W = LT, где L и Т – длина и осадка бревна.
При движении бревен вдоль потока полное сопротивление воды движению состоит из сопротивления формы и сопротивления трения. Полное сопротивление определяется по известной формуле [67]:
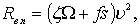(7.57)
где z – коэффициент сопротивления формы, z = 0,98;
f – коэффициент сопротивления трения, f = 0,099;
W – площадь миделевого сечения бревна;
S – площадь трения.
В формуле (7.57) первый член есть сопротивление формы круглой пластины, поставленной нормально к потоку, а второй – увеличение сопротивления с ростом удлинения цилиндра 1/d .
Поэтому зависимость (7.57) для определения сопротивления бревна, расположенного вдоль потока, может быть записана следующим образом:
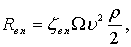(7.58)
где zв.п – коэффициент сопротивления, зависящий от отношения 1/d, может быть определен по формуле:
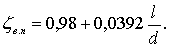(7.59)
При движении в водном потоке группы бревен /щети/ меняются условия обтекания бревен, следовательно, сопротивление щети бревен нельзя определить простым суммированием сопротивлений одиночных бревен.
Как показали опыты, при движении бревен без интервалов, т.е. сплошной щетью, при одной и той же скорости буксирования:
сопротивление двух бревен, расположенных вплотную рядом, на 25% меньше сопротивления одного бревна;
при увеличении числа бревен до 10 штук сопротивление щети становится равным сопротивлению одного бревна;
при увеличении числа бревен до 20 штук сопротивление щети увеличивается на 50% по сравнению с сопротивлением одного бревна.
С увеличением интервалов между бревнами щети условия обтекания изменяются.
Сопротивление движению поперечного ряда /щети/ бревен определяется по формуле
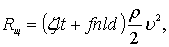(7.60)
где l, t, d – длина, осадка, диаметр бревна;
n – число бревен;
f – коэффициент сопротивления трению, f = 0,025;
z – коэффициент сопротивления формы, зависящий от числа бревен, определяемый по таблице 7.2.
Таблица 7.2
| Число бревен | n | 1 | 2 | 3 | 5 | 10 | 20 |
| Коэффициент сопротивления | z | 0,88 | 0,59 | 0,49 | 0,43 | 0,41 | 0,39 |
В формуле (7.60) первый член при n = 1 – лобовое сопротивление прямоугольной пластины, расположенной нормально к потоку, а второй – сопротивления трения. При увеличении числа бревен улучшаются условия их обтекания, т.к. второе и последующие бревна находятся в спутном потоке за первым бревном и не испытывают лобового сопротивления. С ростом числа бревен сопротивление формы уменьшается и происходит увеличение сопротивления трения, т.е. растет второй член уравнения (7.60).
Таким образом, сопротивление движению одиночного бревна, расположенного вдоль потока, может быть определено по формуле (7.58), поперек потока – по формуле (7.56), сопротивление щети бревен–по формуле (7.60).