Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

7.6.1 Присоединенная масса тела

Неустановившееся движение лесотранспортной единицы можно представить уравнением

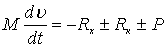,  (7.92)

где P – внешняя сила;

 R_x – сила гидравлического сопротивления жидкости движению тела;

 R_к – гидродинамическая сила, вызванная дополнительным сопротивлением присоединенной массы воды;

 М – масса тела;

 du/dt – ускорение тела, при du/dt > 0 наблюдается разгон, при du/dt < 0 – торможение движению тела. Рассмотрим природу возникновения присоединенных сил. Предположим, что тело под действием внешних сил движется в неподвижной вязкой жидкости в направлении оси X с переменной скоростью (рисунок 7.11). Тогда вследствие наличия сил  вязкости тело выводит из состояния покоя прилегающие к нему частицы жидкости, а те соседние с ним частицы [68], [80].

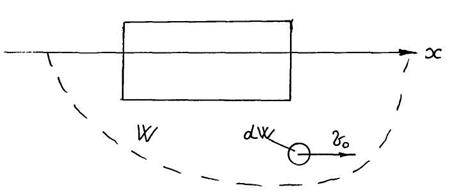
Рисунок 7.11

Таким образом, жидкость в объеме W приходит в движение. Следовательно, часть энергии, прикладываемой к телу извне, расходуется не только на преодоление сил инерции самого тела, но и на изменение кинетической энергии в жидком объеме W. Выделим из него элементарный объем dW с массой rdW, определим элементарный запас его кинетической энергии:

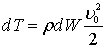,  (7.93)

где u₀ – скорость движения элементарного объема жидкости dW.

Кинетическую энергию всего объема W, выведенного из состояния покоя, получим, интегрируя значение (7.93):

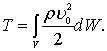  (7.94)

Преобразуем полученный интеграл, умножив и разделив его на квадрат мгновенной скорости движения тела u:

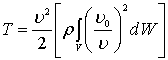.  (7.95)

Выражение в квадратных скобках имеет размерность массы и называется присоединенной массой:

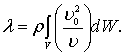  (7.96)

Подставив выражение (7.96) в (7.95), получим

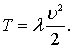  (7.97)

Из этого выражения следует, что присоединенной массой называется такая фиктивная масса жидкости, кинетическая энергия которой при ее движении со скоростью тела равна кинетической энергии окружающей тело жидкости. Присоединенная масса зависит от формы погруженной в жидкость части тела и направления движения.

Определим силу динамического воздействия со стороны жидкости на тело. При движении вдоль оси X тело совершает работу, т.е. можно записать

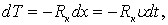  (7.98)

где  R_к – проекция на ось X равнодействующей сил инерции масс жидкости, выведенной телом из состояния покоя.

Знак минус в правой части выражения (7.98) вызван тем, что согласно закону Ньютона, со стороны тела на жидкость действует отрицательная сила R_к.

Из выражения (7.98) следует

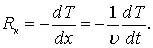  (7.99)

Дифференцируем выражение (7.99), полагая, что присоединенная масса не зависит от времени: 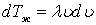. Полученное выражение подставляем в выражение (7.99):

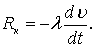  (7.100)

Таким образом, можно считать установленным, что сила динамического воздействия со стороны жидкости на тело R_к при ускоренном движении численно равна присоединенной массе, умноженной на ускорение тела. Поскольку эта сила пропорциональна ускорению, она называется инерционной силой.

Если тело движется равномерно, то du/dt = 0, и, следовательно, инерционная гидродинамическая сила отсутствует. Поскольку присое диненная масса l, как и масса вообще, величина скалярная, знак инерционной силы определяем знаком ускорения. При положительном ускорении R_котрицательна, то есть играет роль силы сопротивления.

Подставляя выражение (7.100) в уравнение неравномерного движения тела в жидкости (7.92), получим

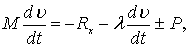
перенеся второй член правой части в левую часть, получим

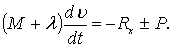  (7.101)

При движении тела в реальной жидкости, имеющей свободную поверхность, понятие о присоединенной массе носит несколько условный характер. Под присоединенной массой в этом случае понимают величины, оказывающие на движение тела такое же воздействие, как и присоединенные массы при движении тела в безграничной идеальной жидкости. Установлено, что в отличие от присоединенных масс, эти величины в той или иной мере зависят от характера движения тела – скорости, ускорения, предыстории движения и т.п.

Величину присоединенной массы определяют экспериментальным путем. Теоретически же присоединенные массы определены только при движении некоторых тел (пластины правильных форм, шар, цилиндр, трехосный эллипсоид) в безграничном потоке идеальной жидкости [80].

Трудность в определении значения присоединенной массы лесотранспортных единиц заключаются в том, что при неустановившемся движении гидродинамическая сила R_х и сопротивление движению тела зависят от его ускорения. Разделить эти силы в процессе эксперимента на отдельные составляющие практически невозможно. Поэтому в целях упрощения практических задач, связанных с неравномерным движением тел в жидкости, предложена гипотеза квазиста ционарности [64].

Согласно этой гипотезе, общее гидравлическое сопротивление жидкости неравномерному движению тела состоит из двух составляющих:

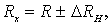  (7.102)

где R – так называемая стационарная часть сопротивления жидкости неравномерному движению тела;

 DR_H – так называемое дополнительное сопротивление, вызванное нестационарностью процесса.

Оказалось, что дополнительное сопротивление DR_H может поразному влиять на процесс неравномерного движения тела, поэтому в формулу (7.102) оно входит с двумя знаками.

Стационарную же часть сопротивления определяют по известной формуле, применимой к равномерному движению:

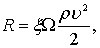  (7.103)

где  x – коэффициент сопротивления, который принимается равным коэффициенту сопротивления равномерного движения тела при скорости u;

u – мгновенное значение переменной относительной скорости движения тела.

Удобство пользования формулой (7.103) состоит в том, что на практике нахождение коэффициента x для тел любой формы не вызывает затруднений.

Что касается дополнительного сопротивления DR_H, то считается, что эта часть гидравлического сопротивления неравномерного движения тела в жидкости зависит в той или иной мере от вида движения (разгон, торможение) и от величины ускорения.

Как было сказано ранее, на практике сила DR_H не может быть отделена от инерционных сил, вызванных присоединенными массами, поэтому ее влияние на динамику неравномерного движения учитывается вместе с влиянием присоединенных масс с помощью безразмерного коэффициента n ,вычисляемого по формуле

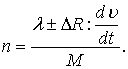  (7.104)

Присоединенная масса l зависит от направления движения тела в жидкости. При поступательном движении тело может перемещаться в направлении одной из трех координатных осей (X, Y, Z), поэтому имеют место три присоединенные массы (l_x, l_y, l_z),

Коэффициент n совокупного влияния на процесс неравномерного движения присоединенной массы тела в идеальной жидкости и нестационарной части гидравлического сопротивления неравномерного движения часто называют просто коэффициентом присоединенной массы [74].

Таким образом, гипотеза о квазистационарности может быть интерпретирована следующим образом. При исследовании неравномерного движения тела по свободной поверхности потока реальной жидкости или вблизи от нее гидравлическое сопротивление его движению принимается таким же, как и при равномерном движении со скоростью, численно равной мгновенным значениям скорости неравномерного движения. Но при этом коэффициент присоединенной массы тела состоит из суммы коэффициента присоединенной массы при движении этого же тела в безграничном потоке идеальной жидкости и добавки к нему, учитывающей нестационарность процесса движения в реальной жидкости и наличие свободной поверхности потока.

Использование гипотезы квазистационарности оказалось весьма эффективным при исследованиях неравномерного движения лесотранспортных единиц, в том числе бревенных пучков и плотов.

Таким образом, с учетом коэффициента присоединенных масс (7.104) уравнение неравномерного движения тела в водном потоке принимает вид (7.101).