Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

8.2 Виды подобия

Понятие подобия первоначально заимствовано из геометрии, где речь шла о геометрическом подобии, например, подобие треугольников: два треугольника подобны, если у них соответственные углы равны и сходственные стороны пропорциональны. Подобие определяет существование некоторых масштабных соотношений, то есть масштабных коэффициентов, характеризующих пропорциональность сходственных параметров.

Рассматривая отношение характерных размеров натурного потока жидкости и потока на модели, можно записать

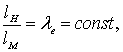  (8.1)

где l_е – масштабный коэффициент или масштаб длин.

Пропорциональность параметров – это лишь частный случай подобия физических процессов. Соблюдение соответствия модели и натуры, отвечающее геометрическому подобию, не раскрывает подобия физических явлений. Физическое подобие достигается при одинаковой физической природе подобных явлений. Физическое подобие требует, кроме геометрического подобия, соблюдения кинематического подобия, при котором существует подобие скоростей и ускорений в соответствующих точках модели и натуры, а также соблюдения дина мического подобия, то есть подобия сил в соответствующих точках модели и натуры.

Физическое подобие может быть полным, неполным и приближенным. Полное подобие – это подобие протекания во времени и пространстве физических процессов, достаточно полно характеризующих изучаемое явление. Обеспечение полного подобия – основная задача исследования. Однако в процессе исследований не всегда удается обеспечить полное моделирование. Исследователи вынуждены прибегать к неполному или приближенному подобию. При неполном подобии обеспечивается подобие исследуемого процесса только во времени или только в пространстве.

В случае приближенного подобия допускается некоторое искажение в отношении какого–либо физического явления на исследуемой модели, допускают независимость влияющих параметров. При этом оценка влияющих параметров производится на основе предварительных оценок или на основе анализа ранее выполненных подобных исследований.

Математическое подобие требует соответствия сходственных параметров сравниваемых процессов различной физической природы, то есть математическое подобие возможно для двух разнородных физических процессов, но описываемыми одними и теми же дифференциальными уравнениями. Такое подобие называют аналоговым. В механике жидкости часто используется электрогидродинамическая аналогия (ЭГДА), газогидравлическая аналогия, гидромагнитная аналогия.

Так, математически подобными будут два уравнения, описывающие физически разнородные процессы, например г уравнение переходного процесса в электрической цепи и уравнение процесса вынужденных механических колебаний в вязкой среде закрепленного на пружине груза.