Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

8.8 Правила моделирования взаимодействия одиночных судов с водной средой

При проведении буксировочных испытаний моделей судов с целью определения сопротивления воды движению необходимо выполнить динамическое подобие, т.е. геометрическое подобие модели и судна, равенство чисел Рейнольдса и Фруда для судна и модели.

При соблюдении условий динамического подобия, сопротивление воды движению судна и модели определяется, согласно общему закону подобия Ньютона

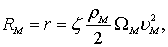
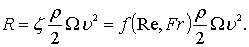  (8.104)

Выполнить одновременно условие подобия по закону Re, Fr практически невозможно. Так, из равенства чисел Rе и Fr для модели и судна получаем следующие выражения для отношения соответственных скоростей

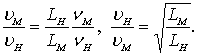
Приравнивая правые части этих равенств, установим связь между масштабом модели 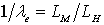 отношением кинематических коэффициентов вязкости жидкости ν_M и ν_Н

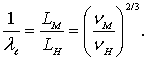  (8.105)

Из равенства (8.105) следует, что при ν_M = ν_Н размеры модели и натуры должны быть равны. Однако подобрать жидкости с такими кинематическими коэффициентами вязкости, которые обеспечивали бы, согласно равенству (8.105), приемлемый для испытания модели масштаб, оказывается практически невозможно.

Поэтому при определении полного сопротивления судна на основе модельных испытаний приходится не учитывать некоторые условия подобия, необходимые для соблюдения полного динамического подобия потоков жидкости.

В основу моделирования надводных судов положено равенство только чисел Фруда для модели и натуры Fr_M = Fr_Н, т.е. в этом случае вязкостная часть сопротивления не моделируется, поскольку не выполняется равенство чисел Rе.

Для определения вязкостной части сопротивления используются приближенные экспериментально-теоретические методы.

Как уже отмечалось выше, изучение сопротивления воды движению судов базируется на гипотезе о разделении полного сопротивления на отдельные независимые составляющие. Этот же принцип положен в основу пересчета результатов испытания моделей на натуру.

Полное сопротивление судна определяется по формуле

R = R_TP +R_OCT,  (8.106)

где  R_TP – сопротивление трения, определяемое в зависимости от чисел Rе;

 R_OCT – остаточное сопротивление, зависящее от чисел Re и Fr.

Сопротивление трения определяется расчетным путем как сопротивление трения эквивалентной технически гладкой пластины, обтекаемой турбулентным потоком

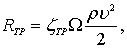  (8.107)

где  Ω – характерная площадь судна;

 ρ – плотность жидкости;

 υ – скорость движения судна; 

 ζ_TP – коэффициент сопротивления трения.

Технически гладкой поверхностью принято считать поверхность, неровности которой практически не оказывают влияние на сопротивление воды движению тела. Под эквивалентной пластиной понимается пластина прямоугольной формы, имеющая длину, равную длине судна или модели по действующей ватерлинии, и смоченную поверхность, равную смоченной поверхности корпуса судна или модели и движущейся в жидкости со скоростью судна (или модели).

Для определения коэффициента сопротивления трения технически гладкой пластины при турбулентном обтекании получила распространение формула Прандтля-Шлихнинга [86,64], согласно которой

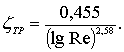  (8.108)

Для модели пластина предполагается технически гладкой, а для натуры поверхность обладает такой же шероховатостью, как и судовая поверхность.

Вторая часть сопротивления – остаточное сопротивление, определяется по модельным испытаниям. Остаточное сопротивление состоит из сопротивления формы (вихревое сопротивление) R_ф и волнового сопротивления R_вол.

Из формулы (8.106) следует, что для судна

R_OCT =R – R_TP. (8.109)

Для модели остаточное сопротивление

r_OCT = r – r_TP, (8.110)

где  r – полное сопротивление модели, измеренное при скорости буксировки υ_M;

 r_TP – сопротивление трения модели, вычисленное как сопроти вление технически гладкой пластины.

Согласно условию динамического подобия, при определении сопротивления путем модельных испытаний Fr_M = Fr_H, тогда и коэффициенты остаточного сопротивления для модели и натуры равны

ζ_OCT.M = ζ_OCT.M.

При моделировании по закону подобия Фруда

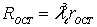.  (8.111)

Сопротивление судна по модельным испытаниям определится из равенства

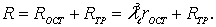  (8.112)

Эта формула была бы справедлива, если бы остаточное сопротивление судна полностью состояло из волнового сопротивления. Так как в остаточное сопротивление входит еще и сопротивление формы (вихревого сопротивления), то для получения более точных результатов необходимо учесть влияние кривизны поверхности корпуса судна R_тр.кр .

При расчете полного сопротивления воды движению судна необходимо учесть ряд поправок. К этим поправкам относятся: дополнительное сопротивление, вызванное шероховатостью обшивки корпуса R_шер, сопротивление выступающих частей R_выс.ч, воздушное сопротивление надводной части судна, дополнительное сопротивление судна, плавающего на взволнованной поверхности R_волн.

Таким образом, с учетом указанных поправок полное сопротивление судна определится

R = R_тр + R_тр.кр + R_шер + R_ост + R_выс.ч + R_возд + R_волн.  (8.113)

Соответственно можно записать, что и коэффициент полного сопротивления судна равен

ζ = ζ _тр + ζ _тр.кр + ζ _шер + ζ _ост + ζ _выс.ч + ζ _возд + ζ _волн.   (8.114)

Рассмотрим каждую составляющую коэффициента полного сопротивления:

ζ _тр – коэффициент сопротивления трения эквивалентной пластины, обтекаемой турбулентным потоком, определяется по формуле Прандтля – Шлихтинга (8.108);

ζ _тр.кр – коэффициент, учитывающий влияние кривизны корпуса судна на сосопротивление трения; для практических расчетов принимают равным (0,01 – 0,04). Обычно при пересчете результатов испытаний модели на судно коэффициент учитывающий влияние кривизны корпуса судна, принимают равным для модели и натуры, т.е.

ζ _тр.кр.м = ζ _тр.кр.н;

ζ _шер – надбавка на шероховатость определяется по результатам натурных буксировок. Для практических расчетов коэффициент надбавки на шероховатость может быть определен по таблице 8.5.

ζ _выс.ч – коэффициент сопротивления, учитывающий сопротивление выступающих частей корпуса (рули, кронштейны гребных винтов, скуловые кили и др.)

Таблица 8.5

У обычных судов при правильно спроектированных выступающих частях коэффициент ζ _выс.ч колеблется в пределах (0,2 – 0,3) × 10^-3; у судов с сильно развитыми выступающими частями и скуловыми килями он может достигать значения (0,3 – 0,5) × 10^-3 [1].

ζ _возд – коэффициент воздушного сопротивления надводной части судна. Абсолютная величина воздушного сопротивления у судов, движущихся при безветрии или при слабом ветре, невелика и составляет от 1,5 до 3,0 % полного сопротивления, однако при наличии ветра роль воздушного сопротивления возрастает и при сильном встречном ветре может достигнуть 10 % и более. Для приближенных расчетов принять ζ _возд = (0,05 ¸0,09) × 10^-3;

ζ _волн – коэффициент дополнительного сопротивления на волнении. Эта составляющая сопротивления учитывает влияние волнения моря на скорость хода судна.

ζ _волн = (0,1 ¸ 0,6) × 10^-3.

Дополнительные коэффициенты сопротивления ζ _возд и ζ _волн вводятся в расчет в зависимости от необходимости учета влияния этих коэффициентов на сопротивление рассматриваемого судна.

Таким образом, моделирование взаимодействия одиночных судов с внешней средой базируется на гипотезе разделения волнового сопротивления на две независимые составляющие – сопротивление трения, определяемое расчетным путем, и остаточное сопротивление, определяемое на модели.

Сущность изложенного метода пересчета сопротивления судна на натуру заключается в следующем:

1. Определяется полное сопротивление модели.

2. Сопротивление трения модели определяют по формуле (8.108).

3. Величина остаточного сопротивления модели находится по формуле (8.110). Определяется коэффициент остаточного сопротивления моделиζ_ост.м. При условии Fr_M = Fr_H, ζ _ост.м = ζ _ост.н.

4. Определяется остаточное сопротивление судна (8.111).

5. Находится сопротивление судна по модельным испытаниям (8.102). Сопротивление трения судна определяется по формуле (8.109).