
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.4.1 Гидродинамически подобные потоки
Условимся называть объект, взаимодействие которого с внешней средой предстоит изучить, – натурой, а соответственно уменьшенный объект, с которым будут проводиться опыты в лабораторных условиях, моделью.
Модель воспроизводит физическое явление таким образом, что результаты исследований на модели с помощью соответствующих масштабных множителей могут использоваться для точного предсказания ожидаемых характеристик натурного явления.
Замена изучения интересующего нас явления в натуре на модели называется моделированием. В основе моделирования лежат общие законы механического подобия. Для полного механического подобия явлений необходимо их геометрическое, кинематическое и динамическое подобие.
Геометрическое подобие служит основой для кинематического и динамического подобия.
Для соблюдения геометрического подобия необходимо и достаточно, чтобы все соответствующие размеры натуры и модели и границ потоков, обтекающих натуру и модель, были пропорциональны, то есть
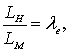 (8.2)
(8.2)
где LM, LH – соответственно характерные размеры модели и натуры;
le – геометрический масштаб модели, показывающий, во сколько раз размеры модели изменены по сравнению с натурой.
Отношение площадей и объемов натуры и модели запишутся
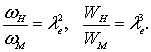 (8.3)
(8.3)
Для соблюдения кинематического подобия потоков необходимо, чтобы скорости в соответствующих точках были пропорциональны друг другу и одинаково направлены по отношению к их границам, то есть траектории движения сходственных частиц жидкости должны быть геометрически подобны
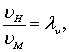
где lu – масштаб скоростей.
Для динамического подобия необходимо, чтобы все силы одинаковой природы, действующие в соответствующих точках, были пропорциональны, то есть
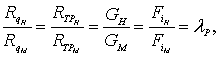 (8.4)
(8.4)
где Rq, RTP – результирующие сил давления и сил трения, действующие на сходные элементы поверхности;
G – результирующая сил тяжести соответствующих объемов жидкости;
Fi – результирующая сил инерции, действующих на соответствующие объемы жидкости;
lP – масштаб сил.
Потоки жидкостей, удовлетворяющие одновременно условиям геометрического, кинематического и динамического подобия, называются гидродинамически подобными потоками.
В гидродинамически подобных потоках силы F, действующие на соответственные точки, находятся в отношении
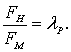
Выразим силу F через массу m и ускорение a, а ускорение через скорость u и путь l:
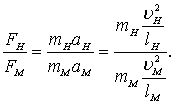 (8.5)
(8.5)
Преобразуем равенство (8.5) следующим образом
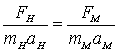 или
или 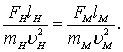 (8.6)
(8.6)
где mH, mM – массы соответсвенных частиц потока в натуре и в модели;
aH, aM – ускорение.
Отношение 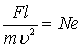 называется числом или критерием Ньютона.
называется числом или критерием Ньютона.
Таким образом, гидродинамическое подобие всегда требует равенства критериев Ньютона для модели и натуры [84]
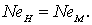
Числовое значение критерия Ньютона зависит от величины сил, масс, скоростей и линейных размеров исследуемой части потока.
Гидродинамическое подобие возможно лишь при наложении не которых условий на динамические и кинематические характеристики потоков. Эти условия называют критериями гидродинамического по добия. Они определяются природой сил изучаемого явления. Для обеспечения динамического подобия необходимо обеспечить равен ство критериев подобия у модели и натуры.
