Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

8.4.3 Подобие потоков в случае преобладающего влияния сил тяжести

В большинстве гидравлических процессов, исследуемых с по мощью модели, присутствуют силы тяжести. Например, течения в ре ках и каналах происходят под действием гравитационных сил, силы тяжести проявляются при изучении перелива воды через водосливы и отверстия, движении потока при установке в реке лесозадерживающих сооружений, движении плохообтекаемых лесотранспортных единиц и судов, при взаимодействии плавающих и стационарных сооружений с волнами и т.п.

Если в рассматриваемом гидравлическом явлении преобладают гравитационные силы, то за критерий подобия принимают критерий Фруда, т.е. действует, так называемый, закон подобия Фруда. Для соблюдения подобия необходимо равенство чисел для модели и натуры, т.е. Fr_M = Fr_H.

Критерии подобия необходимо выражать через характерные для данного потока величины. Так, в случае обтекания тел жидкостью в качестве характерного линейного размера выбирают длину тела в направлении потока. В качестве характерной скорости может быть выбрана скорость движения тела или скорость набегания потока. При моделировании рек обычно используют глубину потока или гидравлический радиус русла. При моделировании процесса обтекания лесотранспортных единиц – отдельных бревен, пучков, плотов в качестве характерного линейного размера может быть выбрана длина тела или его осадка.

Критерий Фруда может быть получен из общего критерия гидродинамического подобия Ньютона. Подставим в уравнение (8.6) силу тяжести,G = mg получим

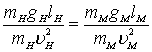 или 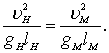  (8.21)

Закон подобия Фруда находит применение при моделировании течений жидкости, имеющей свободную поверхность, так как при этом в значительной мере проявляется действие сил тяжести в жидкости. В таких потоках при равенстве чисел Фруда обеспечивается геометрическое подобие картин волн, возникающих на свободной по верхности при движении тела.

Из равенства (8.21) могут быть получены основные параметры потоков с учетом масштабов подобия. Определим, в какой зависимости находятся скорости, расходы, силы, для модели и натуры в случае моделирования по закону Фруда.

Так как для натурных условий и условий испытания модели ускорение силы тяжести g_H = g_M, то из (8.21) следует:

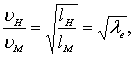 откуда  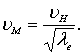 (8.22)

т.е. скорость модельного потока должна быть уменьшена в .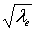

Расходы модели и натуры должны находиться в зависимости

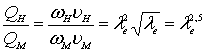 откуда 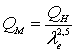,  (8.23)

т.е., если в натуре имеется расход Q_H, то на модели, которая меньше натуры в l_e раз, расход должен быть меньше в 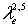 раз.

Силы, действующие на модель и натуру, находятся в соотношении

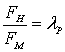 или 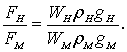  (8.24)

Так как для модели и натуры плотность воды и ускорение силы тяжести можно принять равным, т.е. g_H = g_M и r_H = r_M, то из формулы (8.24) получим

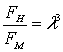, откуда 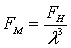.  (8.25)

Подобным же образом можно установить значения масштабных множителей для времени, работы, давления и т.д., выражая их через линейный масштаб l_e.