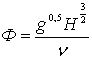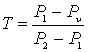Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.4.5 Другие критерии подобия
Большинство гидравлических процессов, связанных с движением однородных жидкостей, взаимодействие этой жидкости с гидротехни ческими, лесосплавными объектами происходит под действием сил тяжести или вязкости. В этом случае моделирование выполняется по критерию подобия Фруда или Рейнольдса.
Кроме критериев подобия Фруда и Рейнольдса, имеется еще ряд определяющих критериев. Рассмотрим некоторые из них.
Критерий Струхаля [88, 89, 90] получен из анализа уравнений (8.11) и (8.19)
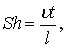
где t – период времени, характерный для установившегося движения на участке l.
Критерий Струхаля необходимо вводить при изучении подобия динамики неустановившихся потоков вязкой жидкости.
Критерий Струхаля вводится в рассмотрение при изучении на модели сопротивления воды неустановившемуся движению судна, плота, пучка, бревна с ускорением при разгоне или торможении.
Критерий подобия Эйлера (8.18) представляет собой отношение давления в данной точке потока к скоростному напору. Следовательно, равенство критериев Эйлера в динамически подобных потоках обеспечивает подобие сил давления.
Критерий Эйлера играет большую роль при моделировании яв лений, связанных с кавитацией, например, при изучении кавитации у гребных винтов путем испытания их моделей. Если движение тела не сопровождается возникновением кавитации, то при соблюдении критериев подобия Fr, Reравенство чисел Eu для модели и натуры обеспечивается.
Критерий подобия Вебера должен учитываться в потоках, в которых значительная роль принадлежит силам поверхностного натяжения:
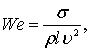 (8.33)
(8.33)
где s – коэффициент поверхностного натяжения жидкости. Влияние поверхностного натяжения должно быть настолько малым, чтобы оно не мешало образованию волн.
Для подобия потоков с учетом сил поверхностного натяжения требуется соблюдение равенства чисел Вебера.
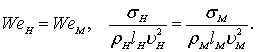 (8.34)
(8.34)
Критерий подобия Коши. При изучении процесса взаимодействия потока с упругими конструкциями возникает необходимость введения критерия подобия, связывающего силы, которые одновременно возникают в потоке и конструкции. Таким критерием служит число Коши:
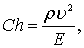 (8.35)
(8.35)
где E – модуль упругости материала конструкции.
Для подобия потоков с учетом сил упругости необходимо соблюдение равенства чисел Коши
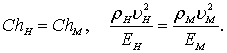 (8.36)
(8.36)
Критерий подобия Маха. При движении сжимаемой жидкости (газа) с большими скоростями в число критериев подобия вводится число Маха
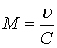 , (8.37)
, (8.37)
где C – скорость волны движения (местная скорость звука в жидкости).
Этот критерий учитывается при исследовании процессов, в которых скорости течения приближаются или превышают скорость распространения звуковых волн в жидкости.
Для подобия потоков с большими скоростями необходимо соблюдение равенства чисел Маха: МH = МM.
Таблица 8.1 Критерии подобия, используемые в механике жидкостей
| №№ Название | Выражение | Область применения |
| 1. Число Фруда | | Относится к действию сил тяжести |
| 2. Число Рейнольдса | | Относится к действию сил вязкости |
| 3. Число Вебера | | Относится к действию сил поверхностного натяжения |
| 4. Число Эйлера | | Учитывается при наличии сил давления |
| 5. Число Коши | | Относится к системе, где важна сжимаемость жидкости |
| 6. Число Маха | | Относится к эффектам сжимаемости в высокоскоростном потоке |
| 7. Число Струхаля | | Относится к случаю неустановившегося движения потоков |
| 8. Число Ричардсона | | Относится к случаям перемешивания или взаимодействия жидкостей; |
| 9. Число Фруда–Рейнольдса | | Комбинированные эффекты сил тяжести и вязкости |
| 10. Число Тома | | Служит параметром кавитации; P1, P2– абсолютные давления на сторонах низкого и высокого давлений гидравлической машины; Pu –давление пара жидкости |
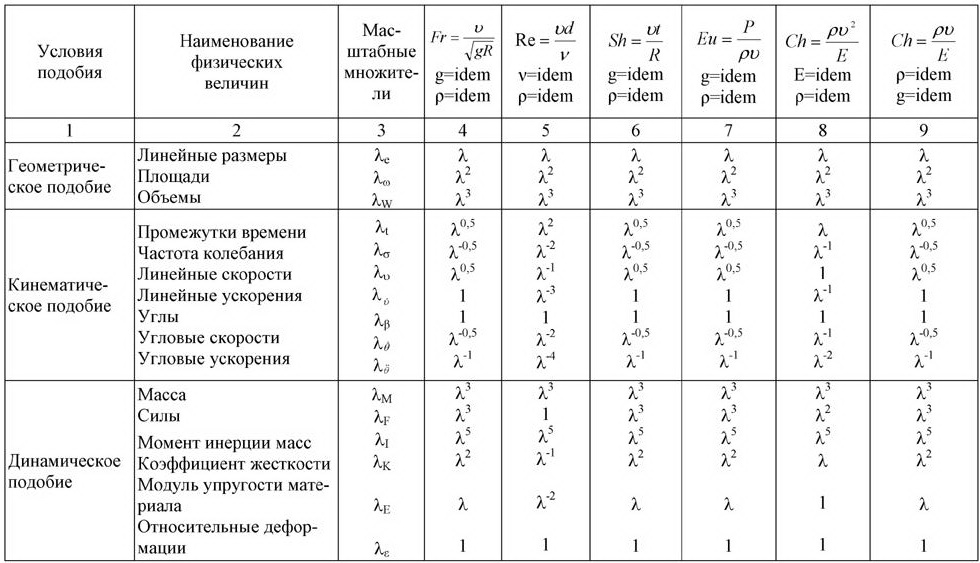
Таблица 8.2 Масштабные множители
Число М играет большую роль в газовой динамике. При М < 1 течение газа называется дозвуковым: оно во многом аналогично течениюнесжимаемой жидкости. При М > 1 течение газа называют сверхзвуковым: оно качественно отличается от течения несжимаемой жидкости. До чисел М < (0,2...0,3) влиянием сжимаемости можно пренебречь.
При движении двухфазных жидкостей (например, вода, насыщенная пузырьками воздуха) скорость звука весьма мала и имеет порядок скорости потока. В этих случаях для подобия потоков необхо димо соблюдение равенства чисел Маха [85].
При пересчете результатов модельных испытаний на натурный объект исследований необходимо иметь масштаб моделирования и масштабные множители. Некоторые из масштабных множителей при моделировании по критерию Фруда и Рейнольдса приведены в параграфах 8.4.3; 8.4.4; 8.4.5.
В таблице 8.1 представлены стандартные безразмерные произведения, используемые в механике жидкостей [91].
В таблице 8.2 приведены значения масштабных множителей для критериев подобия, используемых при проведении исследований вза имодействия водной среды с лесотранспортными объектами и иссле довании гидравлических процессов [92, 93].

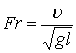
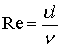
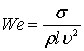
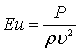
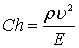
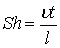
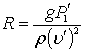
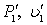 – вертикальные градиенты плотности и скорости
– вертикальные градиенты плотности и скорости