Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

8.5.1 Единицы измерения, размерность

Прежде чем приступить к рассмотрению методики определения критериев подобия на основе анализа размерностей, кратко сформулируем необходимые исходные определения.

1.  Единицей измерения [А] физической величины А является условно выбранная физическая величина а, имеющая тот же физический смысл, что и величина А. Измерение физической величины А сводится к сравнению ее с некоторой одноименной величиной а, принятой за единицу.

В качестве стандарта принят ГОСТ 8.417 – 81 "Единицы физических величин", основу которой составляет Международная система единиц СИ.

2. Различают основные единицы измерения – независимо установленные единицы измерения для произвольно выбранных физических величин и производные единицы измерения.

Производные единицы измерения отражают функциональную взаимосвязь между основными единицами измерения на основе физических законов.

Примерами производных единиц измерения могут быть скорость [υ]=[L]/[T]; равномерное ускорение [a]=[υ]/[Т]=[L][Т]^-2, сила [F]=[m][a]=[M][L][T]^-2.

3.  Размерность физической величины (ГОСТ 16263 – 70) – это выражение, отражающее ее связь с основными величинами некоторой системы величин. Она имеет вид произведения основных величин, возведенных в соответствующие степени. Так, выбрав в механике в качестве основных величин длину [L], массу [М] и время [Т], получаем размерность некоторой величины в виде [x]=L^αM^αT^α. Если все показатели степени равны нулю, величина безразмерна и в отличие от размерных величин не меняет своего значения при изменении размеров используемых единиц.

Размерность любой физической величины представляет собой произведение возведенных в степени размерностей основных единиц измерения.

4.  Различают параметры с независимыми размерностями (независимые параметры) и параметры с зависимыми размерностями (зависимые параметры). Группа независимых параметров – это такая группа параметров, в которой размерность ни одного из параметров не может быть образована из размерностей других параметров, при надлежащей той же группе. Примером группы независимых параметров могут служить группы (l, m, υ) и (m, υ,a), так как

[l]=[L], [m]=[M], [υ]=[LT^-1] ¹ j ([l][m]);

[m]=[M], [υ]=[LT^-1] и [a] ¹ j ([m][υ]).

Параметры групп ( Ђ,Ј,V  )я(ГП;й; F ) являются зависимыми, так как

[l]=[L], [t]=[T], но [υ]=[LT^-1] = j ([l][t]);

[m]=[M], [a]=[LT^-2], но [F]=[ma]=[MLT^-2]= j ([m][a]).

При изучении вопросов моделирования гидравлических явлений обычно рассматриваются функциональные зависимости, параметры которых можно выразить через три основные размерности: масса [М], длина [L] и время [Т]. Размерность любого члена уравнения может быть выражена произведением некоторых степеней М, L, Т.

Однако эта система единиц измерения (М, L, Т) не является основной. Она стала общераспространенной лишь потому, что используемые в ней величины привычны для наших ощущений. То, что можно выбрать другую систему основных измерений, можно увидеть на анализе закона Ньютона:

F=ma (8.38)

где F – сила;

 m – масса;

 a – ускорение.

Уравнение, выраженное в системе размерности, запишется

[F] = [M] [L] / [T]².  (8.39)

то есть это равенство определяет размерность силы в системе единиц массы, длины и времени. Из уравнения (8.39) можно получить размерность массы в другой системе единиц: сила, длина, время

[M] = [F] [T]² / [L].  (8.40)

Размерности параметров, встречаемых при решении гидравличе ских и лесосплавных задач, можно выразить через размерности массы, можно получить из зависимости

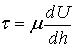,  (8.41)

откуда 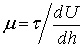, т.е. коэффициент динамической вязкости (динамическая вязкость) пропорционален удельному касательному напряжению и градиенту скорости. Определим размерность

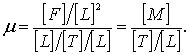  (8.42)

В таблице 8.3 приведены размерности величин, встречающиеся в исследованиях по гидравлике, гидротехнике, гидродинамическом вза­имодействии водного потока с лесосплавными объектами. Размерности величин выражены через массу, длину и время (М, L, Т). При рассмотрении некоторых примеров мы будем использовать параметры, выраженные через силу, длину и время (F, L, Т).

В гидравлических исследованиях часто встречаются задачи, которые невозможно решить теоретически, используя математический аппарат. В этом случае прибегают к эксперименту. Исследователь вскрывает физическую картину изучаемого процесса и может составить полную функциональную зависимость, для раскрытия которой могут быть использованы методы анализа размерностей, входящих в зависимость параметров.