
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.6.1 Основные положения π – теоремы
Развивая теорию анализа размерностей Релея, Букенгем [91], [94] установил правило для нахождения безразмерных комплексов, определяющее любой конкретный физический процесс. Согласно π – теоремы, общую функциональную зависимость, связывающую между собой n переменных величин при N основных единиц их измерения, можно представить в виде зависимости между (n – N) безразмерными комплексами этих величин, а при наличии подобия – в виде связи (n – N) критериями подобия.
Предположим, что функциональная зависимость исследуемого явления известна, и она устанавливает связь n числа размерных физических величин a1, a2, a3,… an (это может быть скорость, плотность, вязкость и т.д.), т.е.
φ = (a1, a2, a3,… an) = 0. (8.46)
Согласно π – теореме, если величины, входящие в зависимость, могут быть выражены через N независимых размерных единиц, то их можно сгруппировать в (n – N) безразмерных комплексов [84 – 98]
φ1(π1, π 2, π 3,… π n-N) = 0, (8.47)
причем число безразмерных комплексов всегда меньше числа исходных величин на (n – N).
Из уравнения (8.47) можно получить значение любого числа в виде
π1 = f (π1, π 2, π 3,… π n-N). (8.48)
В задачах механики жидкости используют три безразмерных единицы – массу, длину, время (М, L, Т ), т.е. N = 3. В этом случае число безразмерных комплексов можно получить выражая числа в виде:
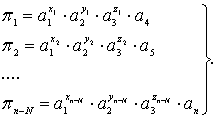 (8.49)
(8.49)
Или для любого числа π
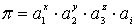 , (8.50)
, (8.50)
где ai – каждая последующая после a3 физическая величина от a4 до an; i = 4; 5...
В любом числе π будет N + 1 переменное и только одно переменное меняется от числа к числу. В каждом числе имеется три неизвестных показателя x, y, z. Рассматривая три независимые размерные величины (М, L, Т), получим три независимых уравнения; одновременное решение этих трех уравнений дает численное значение для трех показателей.
Для любого физического уравнения, в том числе и для уравнений (8.49), размерность левой и правой частей уравнений должна быть одинаковой. Поэтому, представив число π в виде произведения независимых размерных величин в нулевых степенях, а правую часть уравнения (8.50) – в виде степенного одночлена, получим
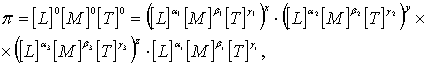 (8.51)
(8.51)
откуда
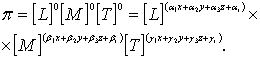 (8.52)
(8.52)
Условие однородности требует равенства показателей степени, т.е.
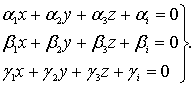 (8.53)
(8.53)
В этих уравнениях γ, β, α – числа, определяемые на основании однородности размерности.
Система уравнений (8.53) решается однозначно относительно показателей степени x, y, z. Решая последовательно каждую строку уравнений (8.49), определяют все безразмерные комплексы π1, π 2, π 3,… π n-N
π – теорема находит применение при исследовании многих задач гидравлики и лесосплава, теоретическое решение которых дает возможность установить только лишь качественную сторону пробле мы.
Для практического использования теоретических зависимостей необходимо введение корректирующих коэффициентов, значения ко торых находятся экспериментальным путем.
