
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.7.1 Определение общего вида формулы сопротивления воды движению полупогруженного тела
В современной гидромеханике аналитическое выражение для определения силы полного сопротивления движению тела в воздушной или водной среде, отвечающее принципам гидродинамического подобия, имеет вид
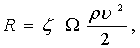 (8.54)
(8.54)
где R – полная сила сопротивления воды движению тела;
ζ – безразмерный коэффициент сопротивления;
ρ – плотность среды;
Ω – характерная площадь тела;
υ – относительная скорость движения тела.
Требуется установить зависимость для определения силы сопротивления движению тела, используя метод показателей.
1. Записываем функциональную зависимость для определения силы сопротивления
R = f (ρ, l, υ, μ, g) (8.55)
где l – длина тела;
μ – динамическая вязкость;
g – ускорение свободного падения.
Размерность входящих в зависимость (8.55) параметров является сочетанием трех основных единиц измерения [ М ],[ L ] и[Т].
2. Возведем в соответствующую степень каждый из определяющих параметров зависимости (8.55)
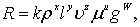 (8.56)
(8.56)
где k – безразмерный коэффициент пропорциональности;
x, y, z, u, w– пять неизвестных показателей степени.
3. Подставим размерности входящих в равенство параметров, пользуясь принятой системой основных единиц измерения (таблица 8.1),
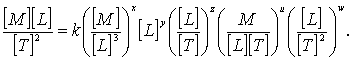 (8.57)
(8.57)
4. Независимо от системы единиц измерения, в которой выраже ны все входящие в уравнение (8.57) параметры, размерность левой части и итоговая размерность произведения правой части уравнения (8.57) должна быть одной и той же.
Условие однородности требует, чтобы показатели степени для каждой из трех единиц измерения [М], [L], [Т] были одинаковы и в левой и в правой частях уравнения (8.57), т.е.
| для массы [М] | |
| для длины [L] | |
| для времени [Т] |
Из системы уравнений (8.58) получим
х = 1 – u; y = 2 – u + w; z = 2 – u – 3w.
Подставив найденные значения показателей х, у ,z в формулу (8.56), получим
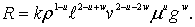
Произведя перегруппировку множителей по показателям, получим
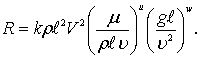 (8.59)
(8.59)
В этой формуле
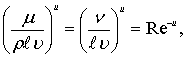
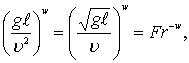
где Re – число Рейнольдса;
Fr – число Фруда.
В формуле (8.59) произведение Re-u, Fr-w можно записать в виде некоторой функции f(Re, Fr) тогда окончательное выражение для определения сопротивления воды движению тела примет вид
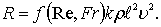
Обозначим f(Re, Fr) = ζ, ![]() 2 = Ω, принимая значения к = 0,5, получим
2 = Ω, принимая значения к = 0,5, получим
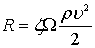 .
.
Общий вид формулы для определения сил сопротивления, полученной на основе теории размерности, идентичен зависимости, отвечающей принципам гидродинамического подобия (8.54). В этих формулах безразмерный коэффициент ζ называется коэффициентом сопротивления тела. Коэффициент сопротивления является сложной функцией, зависящей одновременно от чисел Рейнольдса и Фруда.
Таким образом, величина полной гидродинамической силы, действующей на тело, т.е. силы сопротивления воды движению тела, пропорциональна безразмерному коэффициенту сопротивления ζ, скоростному напору ρυ2/2 и характерной площади Ω.

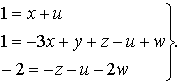 (8.58)
(8.58)