
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.7.2 Определение общего вида формулы сопротивления воды движению полностью погруженного бревна цилиндрической формы
Вывести функциональную зависимость для определения силы сопротивления воды полностью погруженного бревна диаметром D, обтекаемого потоком со скоростью υ. Продольная ось бревна направлена нормально к направлению скорости.
При движении полностью погруженного в воду тела, т.е. при действии Архимедовых сил, течение вокруг него не зависит от сил тяжести. Сила сопротивления обуславливается действием вязкости и силой сопротивления давления, определяемой формой тела.
В этом случае функциональная зависимость запишется
R = f(k, ρ, D, υ, μ)
Введем показатели степени
R = kρxDyυzμu (8.60)
где k – коэффициент пропорциональности.
Запишем уравнение (8.60) в соответствующих размерностях
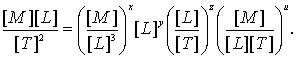 (8.61)
(8.61)
Определяем показатели степени из системы уравнений
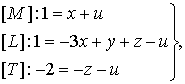
откуда x= 1 - u; y = 2 - u; z = 2 - u.
Введя значение показателей степени в уравнение (8.61) и выполнив перегруппировку, получим
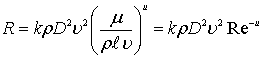 (8.62)
(8.62)
Обозначим Re-u = f(Re), D2 = Ω принимая К = 0,5 , получим
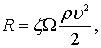 (8.63)
(8.63)
где ζ – коэффициент сопротивления движению полностью погруженного тела; он может быть определен экспериментальным путем.
