
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.7.3 Моделирование силового воздействия волн с плавучим лесосплавным объектом типа плот
Экспериментальные исследования взаимодействия волн с лесосплавными объектами проводятся с целью определения численных значений коэффициентов, необходимых для расчетов динамических нагрузок на лесосплавной объект, например плот, различного типа волногасители.
При этом достоверность полученных результатов зависит от правильного обоснования закона моделирования, условий эксперимента, как-то соотношения определяющих эксперимент факторов и габаритов опытового канала, т.е. правильности выбора масштаба моделирования, измерительной техники и оборудования.
Для установления закона моделирования воспользуемся π – теоремой.
Функциональное уравнение, определяющее силовое воздействие волн на плавающее тело типа плот, запишется следующим образом [99]
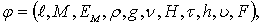 (8.64)
(8.64)
где ![]() , M, Ем – параметры, характеризующие систему:
, M, Ем – параметры, характеризующие систему:
![]() – длина тела;
– длина тела;
М – масса тела;
Ем – модуль упругости якорных связей;
ρ, g, ν, H – параметры характеризующие среду:
ρ – массовая плотность;
g – ускорение свободного падения;
ν – кинематическая вязкость жидкости;
Н – глубина воды;
τ, h, υ, F – параметры, характеризующие возмущение:
τ – период возмущающей силы (волны);
h – высота волны;
υ – максимальная скорость частиц жидкости;
F – сила давления.
В функциональное уравнение входит n = 11 исходных величин, которые могут быть выражены тремя независимыми размерными единицами М, L, Т ( масса, длина, время), т.е. N = 3. В этом случае можно составить (n-N) = 8 безразмерных комплексов, т.е.
φ = (π1, π2,…, π8).
В качестве величин с независимыми формулами размерностей выберем группу ![]() , υ, ρ. В этом случае значения запишутся
, υ, ρ. В этом случае значения запишутся
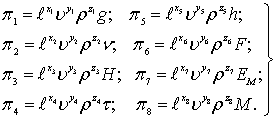 (8.65)
(8.65)
Составим матрицу размерных переменных
| g | ν | H | τ | h | F | Ем | М | υ | ρ | | |
| [M] | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| [L] | 1 | 2 | 1 | 0 | 1 | 1 | -1 | 0 | 1 | -3 | 1 |
| [Т] | -2 | -1 | 0 | 1 | 0 | -2 | -2 | 0 | -1 | 0 | 0 |
Ранг матрицы равен 3, число независимых безразмерных произведений равно 11 – 3 = 8.
Выражения формул размерностей исходных величин запишутся:
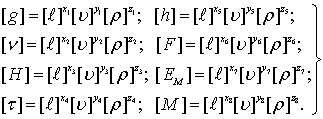 (8.66)
(8.66)
Для любого уравнения (8.65) размерность левой и правой частей уравнений должна быть одинаковой. Поэтому, представив число π в виде произведения независимых размерных величин в нулевых степенях, а правую часть уравнений в виде степенного ряда и приравнивая показатели степеней для трех единиц измерения [М], [L], [Т], можно определить значение показателей xi, yi, zi в уравнениях (8.65).
Матрица показателей степеней для уравнений (8.65) запишется:
| π1 | π2 | π3 | π4 | π5 | π6 | π7 | π8 | |
| xi | -1 | 1 | 1 | 1 | 1 | 2 | 0 | 3 |
| yi | 2 | 1 | 0 | -1 | 0 | 2 | 2 | 0 |
| zi | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Подставляя значение показателей степени в формулы (7.65), по лучим безразмерные комплексы:
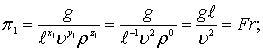 (8.67)
(8.67)
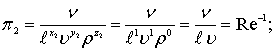 (8.68)
(8.68)
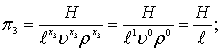 (8.69)
(8.69)
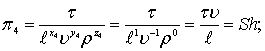 (8.70)
(8.70)
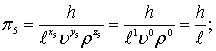 (8.71)
(8.71)
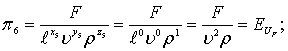 (8.72)
(8.72)
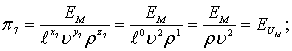 (8.73)
(8.73)
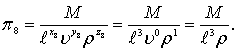 (8.74)
(8.74)
С учетом определенных безразмерных комплексов (8.67 – 8.74), исходное уравнение в критериальной форме запишется
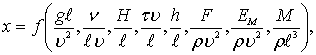 (8.75)
(8.75)
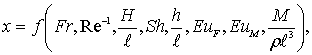 (8.76)
(8.76)
где x – любой замеряемый параметр, представленный в безразмерной форме.
Уравнение (8.75) может быть решено относительно любого замеряемого параметра, например:
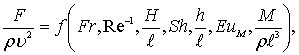 (8.77)
(8.77)
Обозначив через λ линейный масштаб моделирования, параметры уравнения (8.75) могут быть представлены безразмерными соотношениями
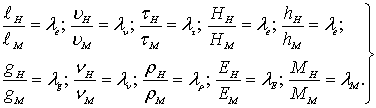 (8.78)
(8.78)
где λi – масштабный коэффициент соответствующего параметра;
Н – натура;
M – модель.
Для подобных явлений безразмерные комплексы, составленные из масштабных коэффициентов (8.78), должны быть равны между собой, т.е. в уравнении (8.75)
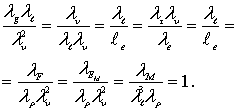 (8.79)
(8.79)
Если лабораторные исследования выполняются в воде, практически не отличающейся по физическим свойствам от натуры, то мас штабные коэффициенты λρ = λд = λg = 1.
Полученное критериальное уравнение в форме (8.76) показывает, что подобие исследуемого процесса взаимодействия волн с пла вающим лесосплавным объектом выполняется при одновременном соблюдении правил (условий) моделирования по законам Fr, Re, Sh, Eu, что практически невозможно обеспечить, т.е. в эксперименте может быть только частичное или неполное подобие исследуемого явления.
Для обеспечения закона моделирования необходимо дать оценку весомости каждого критерия, входящего в уравнение (8.76), рассмотреть физику исследуемого процесса.
Необходимым условием подобия, при котором обеспечивается равенство коэффициентов гидродинамических сил, действующих на модель и натуру, является равенство чисел FrH = FrM, ReH = ReM, т.е.
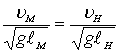 и
и 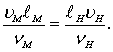 (8.80)
(8.80)
Проверим выполнение этого условия. Из уравнения (8.80) получим
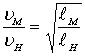 и
и 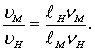 (8.81)
(8.81)
Выражая из уравнения (8.81) значение ![]() M, приравнивая их, получим соотношение
M, приравнивая их, получим соотношение
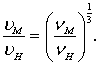 (8.82)
(8.82)
Из выражения (8.82) следует, что при данном масштабе и одновременном соблюдении равенства чисел Re и Fr модели и натуры, скорость обтекания потоком жидкости может отличаться от натуры только в том случае, если эксперименты на модели проводятся в жидкости, вязкость которой отличалась бы от вязкости натурного потока в λ1,5 раз. Это условие в лаборатории практически невозможно выполнить.
В случае проведения экспериментов на модели и натуре в одинаковых жидкостях полное динамическое подобие возможно только при ![]() H =
H = ![]() M.Таким образом, одновременное моделирование по закону Fr и Re силового воздействия волн на лесосплавной объект практически невозможно. Речь может идти только о частичном или неполном моделировании. В этом случае необходимо установить преобладающую силу. Многочисленные исследования утверждают, что волновые процессы обусловлены преобладающим действием сил тяжести [90, 92, 93, 103]. Поэтому правомерен закон моделирования Фруда. Однако действие сил вязкости нельзя не учитывать, т.е. их влияние явно сказывается при изучении волновых процессов на моделях относительно малых масштабов. При моделировании силового воздействия волн необходимо соблюдать условие автомодельности по числуRe. Зоны автомодельности достаточно хорошо изучены для русловых потоков, при движении в круглых трубах. Турбулентность, обусловленная волновым движением жидкости, изучена значительно меньше. В настоящее время уже достаточно убедительно доказано, что к задачам с волновым движением жидкости можно подходить с пози ции оценки его по критическим числам Рейнольдса, т.е. и здесь вполне правомерна аналогия с ламинарным и турбулентными режимами. В этом случае для волнового течения жидкости число Рейнольдса определяют по формуле [93]
M.Таким образом, одновременное моделирование по закону Fr и Re силового воздействия волн на лесосплавной объект практически невозможно. Речь может идти только о частичном или неполном моделировании. В этом случае необходимо установить преобладающую силу. Многочисленные исследования утверждают, что волновые процессы обусловлены преобладающим действием сил тяжести [90, 92, 93, 103]. Поэтому правомерен закон моделирования Фруда. Однако действие сил вязкости нельзя не учитывать, т.е. их влияние явно сказывается при изучении волновых процессов на моделях относительно малых масштабов. При моделировании силового воздействия волн необходимо соблюдать условие автомодельности по числуRe. Зоны автомодельности достаточно хорошо изучены для русловых потоков, при движении в круглых трубах. Турбулентность, обусловленная волновым движением жидкости, изучена значительно меньше. В настоящее время уже достаточно убедительно доказано, что к задачам с волновым движением жидкости можно подходить с пози ции оценки его по критическим числам Рейнольдса, т.е. и здесь вполне правомерна аналогия с ламинарным и турбулентными режимами. В этом случае для волнового течения жидкости число Рейнольдса определяют по формуле [93]
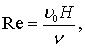 (8.83)
(8.83)
где υ0 – средняя орбитальная скорость по глубине;
H – глубина потока жидкости;
ν – кинематическая вязкость жидкости.
В работе [93] отмечается, что при изучении силового воздействия волн на обтекаемые преграды, к которым можно отнести исследуемый в работе объект, зона автомодельности устанавливается при значении чисел Rе ³ 105 для преград с гладкой поверхностью. Обтекание шероховатого цилиндра и пластины происходит в автомодельной области. Лесосплавной объект строится, как правило, из неокоренных бревен, имеет шероховатую поверхность, т.е. обтекание его волновым потоком происходит в турбулентном режиме, следовательно, условия автомодельности практически соблюдается.
Таким образом, правомерно моделировать силовое воздействие волн на лесосплавной объект по закону подобия Фруда, т.е. возможно частичное моделирование.
Моделирование процесса взаимодействия лесосплавного объекта с системами волн, являющегося нестационарным, в котором основную роль играют силы давления, силы тяжести и силы инерции, производится при соблюдении законов подобия Струхаля и Фруда, причем первый автоматически выполняется при соблюдении второго [86] т.к. инерционные силы совместимы с любыми критериями подобия [92] [104]. Из равенства чисел Струхаля и Фруда для модели и натуры
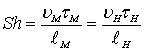 ;
; 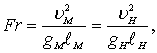
получим
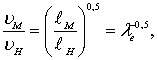 (8.84)
(8.84)
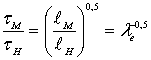 , (8.85)
, (8.85)
т.е. условия подобия нестационарности или периодичности соблюдается при одинаковых амплитудах и одинаковых начальных условиях.
Достаточным условием моделирования натяжения в якорных связях, включающих упругие силы деформации связей плавучего ле сосплавного объекта, является одновременное соблюдение условий за кона подобий Фруда и Коши [102], т.е.
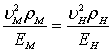 и
и 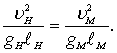 (8.86)
(8.86)
при условии совместное решение уравнений (8.86) дает
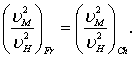 (8.87)
(8.87)
Из уравнения (8.86) получим
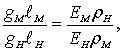 (8.88)
(8.88)
откуда
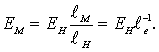 (8.89)
(8.89)
Из выражения (8.89) следует, что условия подобия определяются равенством чисел Фруда для натуры и модели.
На практике возможно приближенное выполнение условий подобия 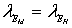 , если вместо стальных тросов в натуре и модели принять капроновые или резиновые тросы.
, если вместо стальных тросов в натуре и модели принять капроновые или резиновые тросы.
В лабораторных условиях практически невозможно соблюсти условия подобия жесткостных характеристик, т.е. обеспечить λd. В работе [93] отмечается ... "как показали многочисленные расчеты систем заякорения различных типов плавсооружений, абсолютные удлинения цепей, вызванные деформацией их звеньев на предельных нагрузках, составляет не более одного процента по сравнению с полными длинами цепей. Это обстоятельство дает основание утверждать, что без существенного влияния на результаты экспериментов можно пренебречь невыполнением условия λd = 1."
Таким образом, при исследовании силового воздействия волн на лесосплавной объект пересчет физических величин с модели на натуру по результатам экспериментальных исследований с достаточной для практики точностью можно производить по закону подобия Фруда.
