
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.7.4 Моделирование волноустойчивости лесотранспортных единиц
При транспортировке лесотранспортных единиц по водохранилищам, ограждении рейдов от воздействия волн обязательно исследуется волноустойчивость лесотранспортных единиц, волноустойчивость защитных сооружений. Из-за сложной взаимосвязи многих факторов, определяющих физический процесс разрушения лесотранспортных единиц (например, речных и озерных плотов, морских плотов – сигар), он не поддается математическому описанию. Такой вывод приводится в работах, касающихся исследований волноустойчивости пучков, озерных и морских плотов [105, 106, 107]. Поэтому волноустойчивость сортиментных хлыстовых пучков и плотов, плавающих волногасителей из хлыстовых пучков определялось экспериментальным путем.
Примем за общий критерий волноустойчивости конструкции (плота, волногасителя) "живучесть" – продолжительность нахождения конструкции при заданном волновом режиме до момента ее разрушения, т.е. способности конструкции противостоять выплыванию хлыстов без разрушения креплений конструкции. В качестве показателя начала разрушения конструкции можно принять выплывание 0,5 % и полное разрушение при 50 % выплывания хлыстов из конструкции [107, 101].
Рассмотрим моделирование волноустойчивости на примере хлыстового пакета, используемого для гашения волн.
Функциональное уравнение запишется:
j = f(c, h, E, ρ, g, ν, λ, h, F, υ, t, t, B), (8.90)
где c, h, E – параметры, характеризующие конструкцию волногасителя;
c = B/hb – коэффициент формы (B, hb– ширина и высота волногасителя);
h – коэффициент полнодревесности волногасителя;
E – модуль упругости материала обвязок волногасителя;
ρ, g, ν – параметры, характеризующие среду;
λ, h, F, υ, t, t – параметры, характеризующие возмущение:
λ, h, t – длина, высота и период волны;
F – натяжение в обвязках;
υ – скорость распространения волны;
t – время размолевывания.
В функциональное уравнение входит 13 исходных параметров, два из которых – безразмерные, 11 исходных параметров могут быть выражены тремя независимыми размерными единицами [M,L,T]. В этом случае можно составить 8 безразмерных комплексов π.
В качестве величин с независимыми формулами размерностей выбираем B, υ, ρ, тогда значения π запишутся:
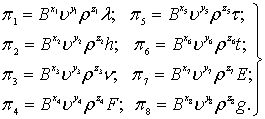 (8.91)
(8.91)
Составим матрицу размерных переменных
| λ | h | ν | F | t | t | E | ρ | g | υ | B | |
| [М] | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| [L] | 1 | 1 | 2 | 1 | 0 | 0 | -1 | -3 | 1 | 1 | 1 |
| [Т] | 0 | 0 | -1 | -2 | 1 | 1 | -2 | 0 | -2 | -1 | 0 |
Определенные значения показателей степеней в уравнениях (8.91) приведены ниже в таблице
| π1 | π2 | π3 | π4 | π5 | π6 | π7 | π8 | |
| xi | 1 | 1 | 1 | 2 | 1 | 1 | 0 | -1 |
| yi | 0 | 0 | 1 | 2 | -1 | -1 | 2 | 2 |
| zi | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
Подставляя значения показателей степеней xi, yi, zi в формулы (8.91), получим
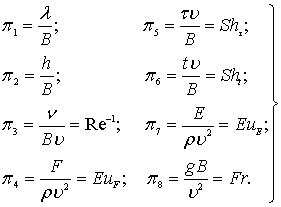 (8.92)
(8.92)
Исходное функциональное уравнение (8.90) с учетом полученных значений πi запишется:
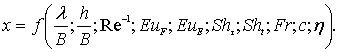 (8.93)
(8.93)
Решая критериальное уравнение (8.93) относительно Sht, получим
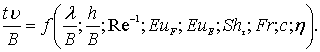 (8.94)
(8.94)
Анализ уравнения (8.94) показывает, что полное подобие модели и натуры при исследовании объекта на волноустойчивость возможно лишь при одновременном соблюдении правил моделирования по закону Re, Fr, Sh, Eu. Давая оценку весомости каждого из критериев подобия, можно доказать, как и в случае силового воздействия волн на плавающий лесосплавной объект, что при исследовании волноустойчивости конструкции на модели при пересчете результатов экспериментов на натуру справедлив закон подобия Фруда.
