Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

8.7.6 Правила моделирования взаимодействия пучковых плотов с водной средой

При выборе правила моделирования взаимодействия пучковых плотов с внешней средой руководствуются двумя методами.

Первый – полный метод, когда необходимо создать модель, полностью соответствующую натуре, предусматривает моделирование геометрических размеров плота, структурных факторов, движителя, длины буксирного троса, ветроволнового режима и др.

Второй – упрощенный метод, когда создается упрощенная модель, на основе которой исследуются только отдельные составляющие возникающих сил сопротивления или влияние отдельных факторов. Этот метод заключается в создании таких моделей взаимодействия, на основе которых можно было бы изучать отдельные составляющие сопротивления.

Полный метод применим, например, когда необходимо провести исследования существующего и проектируемого объекта. Применительно к плотам при этом методе нужно подобрать крупность зерна эквивалентной шероховатости, смоделировать величину и характер расположения выступов местной шероховатости, движитель, длину буксирного троса, ветроволновой режим и др. параметры.

При создании модели взаимодействия по упрощенному методу моделирование крупности зерен общей шероховатости, выступов местной шероховатости и расположения пусков в рамке плота производить не следует. Модель плота рационально изготовлять из пучков с одинаковой осадкой и устанавливать пучки без интервалов по длине и ширине плота. Коэффициент сопротивления общей шероховатости модели плота определяется по крупности зерна шероховатости модельных бревен.

Выбор правила моделирования рассмотрим на примере опреде ления сопротивления воды движению пучкового плота.

На основе гипотезы Фруда, сопротивление воды движению полупогруженного тела в общем виде можно представить как сумму трех сопротивленийтрения, формы и волнового.

Первые две составляющие – сопротивления трения и формы – обуславливаются свойствами вязкости жидкости и являются функцией числа Re.

Волновое сопротивление определяется силами гравитационного характера и зависит от числа Фруда. Дадим количественную оценку каждого вида сопротивления применительно к пучковым плотам. Можно считать, что сопротивления трения и формы в плотах являются преобладающими, а волновое сопротивление – сравнительно невелико.

Покажем это на следующих примерах.

В формулу волнового сопротивления твердого тела, движущегося в водной среде, входит коэффициент волнового сопротивления, являющийся функцией числа Фруда по длине тела.

Известно, например, что при числах Фруда 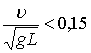 волновым сопротивлением в судах практически можно пренебречь [84,98]. В силу этого, при низких скоростях буксировок плотов волновое сопротивление не будет оказывать практического влияния. Например, при длине плота L = 700 м υ = 0,8 м/с число Fr =0,0098. А при L = 350 м и υ = 0,8 м/с Fr = 0,0143 [23].

Имеющиеся в технической литературе данные относительно роли отдельных составляющих в общем сопротивлении судна показывают, что сопротивление формы составляет значительный процент, особенно в судах несамоходных.

В.В. Звонков [23] приводит данные по динамометрированию речной баржи с размерами: L = 110 м; В = 16 м; Т = 3,0 м, которые показывают, что при некоторых скоростях буксировки баржи сопротивление формы (вихревое) достигает 28 % от общего и 83 % от остаточного и в 3,5 раза превышает волновое.

В.М. Лаврентьев отмечает, что сопротивление формы самоходных судов составляет 5–15 % от полного сопротивления [21].

В литературных источниках дано обоснование пересчета на натуру по гравитационному закону подобия всего остаточного сопротивления судна, значительную часть которого составляет сопротивление формы.

Схема пересчета данных экспериментальных исследований сопротивления движению пучковых модельных плотов на натуру представляется в следующем виде (в дальнейшем эту схему пересчета будем называть 1–м способом).

1. Определяется расчетом сопротивление трения модели плота

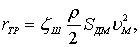  (8.99)

где  ζ_Ш – коэффициент сопротивления трения, зависящий от длины модели плота и крупности зерна шероховатости [21].

2. Из полного сопротивления  воды движению модели вычитается определенное расчетом r_тр и находится вихревое сопротивление модели плота

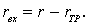  (8.100)

3. Определяется вихревое сопротивление плота в натуре по критерию Фруда

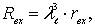  (8.101)

где  λ – геометрический масштаб модели плота.

4. Вычисляется сопротивление трения натурного плота

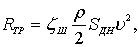  (8.102)

где S_ДН – эквивалентная площадь трения.

5.  В результате суммирования R_вх и R_ТР определяется общее сопротивление натурного плота без учета влияния движителя, выступов местной шероховатости плота, интервалов между пучками по длине и характера их расположения в рамке плота.

6.  Для  получения полного сопротивления плота необходимо учесть добавочное сопротивление от движителя, местной шероховатости, интервалов между пучками по длине и характера их расположения в рамке плота.

Если коэффициенты сопротивления трения от общей шероховатости модельного и натурного плота равны или близки между собою, пересчет данных модельных исследований на натуру производится по критерию Фруда

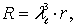  (8.103)

где  R – сопротивление натурного плота без учета влияния выступов местной шероховатости и расположения пучков в рамке плота.

При определении полного сопротивления натурного плота в этом случае также учитывается надбавка в сопротивлении от движителя, выступов пучков и характера их расположения в рамке плота. Эту схему пересчета будем в дальнейшем называть II способом.

I и II способы пересчета справедливы также и при лабораторных исследованиях ветрового сопротивления пучковых плотов ввиду общности физической природы взаимодействия тел с воздушной и водной средой.

По II способу можно вести пересчет на натуру волновых давлений на плот, ввиду гравитационной природы этого вида сопротивлений. При этом необходимо учитывать "масштабные поправки", которые зависят от сил вязкости и трения, отличия трехмерного натурно го волнения от лабораторных волн.

Масштаб моделей плотов необходимо выбирать из условия создания турбулентного режима обтекания плота и размеров опытового бассейна. Сопротивление трения модели плота обуславливается режимами движения жидкости в пограничном слое, а эти режимы зависят от числа Rе и иногда трудно учитываемых случайных обстоятельств, сопутствующих опыту.

Числа Re, относительную шероховатость, обеспечивающие турбулентное обтекание модельных и натурных плотов, можно найти по графику на рисунке 3 в работе [71].

При лабораторных исследованиях сопротивления воды движению судов для надежности измерений прибегают к двум основным приемам:

1. Намеренно выходят из зоны неустойчивых режимов в области больших чисел Rе, заведомо соответствующих турбулентному режиму. Для моделей судов, как показали исследования, эти числа Re лежат в диапазоне 3×10⁶– 6×10⁶.

2. Искусственно турбулизируют пограничный слой, создавая возмущения в передней части модели с помощью плотно примыкающего кольца из проволоки. В этом случае становится возможным снижать указанный диапазон чисел Rе.

Ввиду того, что модель плота, по сравнению с моделью судна, является плохо обтекаемым телом, имеющим свободу перемещения отдельных составляющих частей, прибегать к искусственной турбули–зации нет необходимости – возмущения в пограничном слое модели плота будут создаваться не только в ее передней части, но и по всей длине.