Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.2. КЛАССИФИКАЦИЯ КРИТЕРИЕВ ОПТИМАЛЬНОСТИ

Основная проблема постановки задачи оптимальности - формулировка целевой функции (ЦФ). Все выходные параметры являются функциями внутренних параметров и, следовательно, не могут изменяться независимо друг от друга. Среди них всегда можно найти такие параметры, что улучшение одного из них приводит к ухудшению другого. Такие параметры называются конфликтными.

Если среди выходных параметров можно выделить параметр, наиболее важный и наиболее полно характеризующий свойства объекта, то его естественно и принять за ЦФ. Это частный критерий. В большинстве частных критериев в качестве ЦФ принимают один из выходных параметров, все остальные выходные параметры в виде соответствующих условий работоспособности относят к ограничениям. Например, при проектировании космического аппарата (КА) применяют критерий начальной массы аппарата при заданной массе полезного груза, поскольку она в значительной степени влияет на стоимость выведения КА на орбиту. Следовательно, минимизируются затраты топлива. Применяются, например, ограничения типа равенств на угловую дальность (траекторию) и неравенств на время полета.

Однако в большинстве случаев отдать предпочтение одному среди качественно разнородных величин довольно трудно, поэтому прибегают к построению комплексного критерия, при котором ЦФ объединяет все или большинство выходных параметров. Рассмотрим наиболее распространенные из комплексных критериев.

Мультипликативные критерии. Они могут применяться в тех случаях, когда в ТЗ отсутствуют условия работоспособности типа равенства и выходные параметры не могут принимать нулевые значения.

Тогда ЦФ, подлежащая максимизации, имеет вид:

f(x) = ,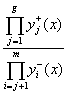

где: ‘+' - ограничения, при которых необходимо максимальное увеличение функции;

  ‘-' - ограничения, при которых необходимо минимизировать функцию.

Удобство этого критерия в том, что не требуется нормирования.

Например, к числу указанных ограничений в ряде задач относятся: ‘+'- КПД, мощность; ‘-' - габариты, вес.

Аддитивные критерии. В аддитивных критериях целевая функция образуется путем сложения выходных параметров, преобразованных к безразмерным слагаемым. Это осуществляется с помощью введения нормирующих множителей - весовых коэффициентов. Нормирование необходимо для объединения нескольких выходных параметров, имеющих в общем случае различную физическую размерность. Тогда ЦФ имеет вид:

f(x)= ω_j y_j(x),

где ω_j - весовой коэффициент, определяемый самим инженером или группой экспертов.

Статистические критерии. Оптимизация имеет целью получения максимальной вероятности Р выполнения условий работоспособности. Эту вероятность и принимают в качестве ЦФ. Например, применение статистического критерия позволяет добиться наименьшего процента брака при серийном производстве спроектированных изделий, т. е. получить максимальную серийную пригодность, или, используя статистические данные по старению, можно получить объекты, имеющие высокую надежность.

Максимальные (минимальные) критерии. Введем количественную оценку степени выполнения  j-го условия работоспособности, обозначим ее через Z_j и назовем запасом работоспособности параметра  y_j. Расчет запаса по j-му  выходному параметру можно выполнить различными способами, например:

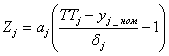
где  - весовой коэффициент;

- номинальное значение j-го   выходного параметра;

- величина, характеризующая разброс j-го выходного параметра. Рекомендуется 5 ≤≤ 20.

Если в качестве целевой функции рассматривается запас только того выходного параметра, который в данной точке x является наихудшим с позиции выполнения требований ТЗ, то:

f(x)= min (x), 1≤ j  ≤ m.

где m - количество запасов работоспособности.

Поэтому ставится задача о выборе такой стратегии поиска x, которая максимизировала бы минимальный из запасов, т. е.

max f(x)=max min  (x),  1 ≤  j ≤ m,  x  XД,

где XД - допустимая для поиска область.

Задача оптимизационного проектирования технических объектов в некоторых случаях можно сформулировать как задачу безусловной оптимизации (без ограничений), но наиболее типичной является условия оптимизации, дающая условие целевой функции при наличии ограничений.

В зависимости от диапазона исследования различают методы локальной и глобальной оптимизации, которые могут и не совпадать.

В зависимости от порядка используемых производных целевой функции по управляемым параметрам методы оптимизации делят на методы нулевого, первого и второго порядков. В методах нулевого порядка (прямых методах) информация о производных не используется. Для методов первого порядка необходимо вычислять как значение функции качества, так и ее первые частные производные (градиентные методы). В методах второго порядка организация поиска экстремума ведется с учетом значений целевой функции, ее первых и вторых производных.

В зависимости от количества управляемых параметров ЦФ различают методы одномерного и многомерного поиска. В зависимости от вида ММ при решении задач оптимального проектирования можно использовать следующие методы: исследование функций классического анализа; метод множителей Лагранжа; вариационное исчисление; принцип максимума Понтрягина; динамическое программирование; линейное программирование; нелинейное программирование; методы случайного поиска и др.

Все градиентные методы используют особенности поведения градиента, которые заключаются в том, что градиент ортогонален к гиперповерхности целевой функции в точке его определения и это направление совпадает с локальным направлением наибыстрейшего возрастания целевой функции. Способ выбора шага, направления поиска или того и другого одновременно определяют сущность метода. Особенностью метода наискорейшего спуска является движение с оптимальным шагом, рассчитанным с помощью одномерной минимизации целевой функции по шагу вдоль антиградиентного направления. Действительно, если в какой - либо точке x направление поиска определено, то целевая функция может считаться функцией переменного параметра шага, характеризующего положение новой точки на x заданной прямой. Поэтому алгоритм метода наискорейшего спуска содержит следующие этапы.

• 1. Вычисление частных производных целевой функции по управляемым параметрам в исходной или промежуточной точке.
• 2. Нахождение одним из методов одномерного поиска оптимального вдоль антиградиентного направления.
• 3. Вычисление координат новой точки x.

Движение прекращается вдоль одного направления, когда линия направления поиска становится касательной к какой - либо линии равного уровня. Каждое направление движения к экстремуму ортогонально предшествующему, если ЦФ квадратичная.

В отличие от градиентных, методы поисковой оптимизации хорошо программируются и требуют меньших затрат машинного времени. Для них характерен выбор направления поиска оптимума по результатам последовательных вычислений ЦФ. По способу точки испытаний ЦФ поисковые методы оптимизации делятся на детерминированные методы поиска и методы случайного поиска. В детерминированных методах переход их предыдущей точки в последующую происходит в соответствии с некоторым алгоритмом, определяющим тот или иной метод. В методах случайного поиска в этот процесс вносится некоторый элемент случайности.

Рассмотрим работу одного из детерминированных методов, предложенный Вудом. Метод поочередно реализует две стратегии поиска: «исследующий поиск» и «поиск по образцу». Вначале задаются исходными значениями элементов x, а также элементов вектора приращений Δx. «Исследующий поиск» заключается в следующем. Циклически по каждой переменной x вычисляют значение целевой функции для  x_i + Δ x_i и x_i  - Δ x_i  , оставляя при этом остальные переменные неизменными. Если окажется, что значение ЦФ улучшается при изменении x на величину  ± Δ x_i , то новое значение фиксированной переменной принимают равным  x_i + Δ x_i или x_i  - Δ x_i  . Аналогичные действия выполняют и для остальных переменных.

После проведения одного (или более) «исследующего поиска» переходят к стратегии «поиска по образцу», заключающейся в следующем. В направлении вектора, определяемого изменениями переменных, которые улучшают значение целевой функции, делают несколько ускоряющихся шагов до тех пор, пока значение ЦФ продолжают уменьшаться. Длину  шага при «поиске по образцу» для ускорения увеличивают пропорционально числу удачных шагов введением некоторого множителя. Если «поиск по образцу» после серии удачных шагов перестает улучшать значение целевой функции, то возвращаются к стратегии «исследующего поиска».

Описанный поиск прекращается при выполнении одного из следующих трех условий:

• 1) ЦФ достигает некоторого заранее установленного значения;
• 2) значения ЦФ оказываются меньше заранее определенных чисел (в задаче минимизации);
• 3) разность между последним и предыдущим значениями ЦФ не превышают некоторого заранее установленного уровня.

Идея методов случайного поиска заключается в том, чтобы перебором совокупностей случайных значений управляемых параметров найти оптимальное значение ЦФ. В отличие от детерминированных методов, в методах случайного поиска направления поиска выбираются случайными на основе генерации в ЭВМ псевдослучайных чисел посредством специальных программ.

Среди многих разновидностей методов случайного поиска простейшим будет слепой поиск (метод Монте-Карло). На (k+1)-м шаге поиска выбирается случайная точка  из допустимой области, вычисляется значение  x _k+1 и сравнивается со значением, полученным на предыдущем шаге. Если , то запоминаются координаты точки и новое значение ЦФ, иначе делается попытка достичь успеха либо изменяя направление на противоположное, либо выбирая новое случайное направление.

Отсутствие универсального метода оптимизации послужило причиной появления множества узкоспециализированных методов, приспособленных к решению отдельных задач. Рассмотрим такие методы, которые можно применить для оптимизаций конструкций элементов и узлов ракетных комплексов.