Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.3. КЛАССИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ФУНКЦИЙ

Такие методы предусматривают собой известные методы дифференциального исчисления. Экстремум целевой функции f(х) находят из необходимого условия его существования, состоящего в том, что производная в точке экстремума равна нулю. Тогда оптимальное решение x^* можно найти из системы уравнений:

.

Для того, чтобы определить, является ли x^* точкой максимума или минимума, используют достаточные условия существования экстремума согласно которым: если производная в точке экстремума меняет знак с плюса на минус, то f(x^*) есть максимум целевой функции; если производная в точке экстремума меняет знак с минуса на плюс, то f(x^*) есть минимум целевой функции.

Если представленные уравнения нелинейные, то решить их систему аналитическим путем удается крайне редко. В этих случаях используют ЭВМ и соответствующие численные методы или методы нелинейного программирования. В последнем случае задачу решения системы сводят к задаче минимизации функции:

.

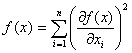Рассматриваемые методы исследования функций классического анализа можно использовать для решения относительно несложных задач оптимизации без ограничений. Однако большинство инженерных задач связано с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой проводится поиск оптимума. На первый взгляд может показаться, что уменьшение размеров допустимой области должно упростить процедуру нахождения оптимума. Однако при наличии ограничений даже может нарушаться условие, в соответствии, с которым оптимум должен достигаться в стационарной точке, характеризующийся нулевым градиентом.

Например, безусловный минимум функции f(x) = (x-2)²  имеет место в стационарной точке x = 2. Но если задача минимизации решается с учетом ограничения  x ≥ 4, то будет найден условный минимум, которому соответствует точка x = 4. Эта точка не является стационарной точкой функции f(x), так как  f ^' (4).