
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
2.4. МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА
Рассмотрим общую задачу оптимизации, содержащую несколько ограничений в виде равенств: минимизировать f(x) при ограничениях gi (x)=0, j=1,...,к.
Эта задача в принципе может быть решена как задача безусловной оптимизации, полученная путем исключения из целевой функции k независимых переменных с помощью заданных равенств. Наличие ограничений в виде равенств фактически позволяет уменьшить размерность исходной задачи с n до n-k. В качестве иллюстрации рассмотрим следующий пример.
Минимизировать f(x)= x1 . x2 + x3 при ограничении: g(x)= x1 +x 2+ x3 - 1 = 0. Исключив переменную x3 с помощью уравнения g(x)=0, получим оптимизационную задачу с двумя переменными без ограничений: f(x1 , x2) = x1 . x2 + (1 - x1 - x2) .
Метод исключения переменных применим лишь в тех случаях, когда уравнения, представляющие ограничения, можно разрешить относительно некоторого конкретного набора независимых переменных. При наличии большого числа ограничений в виде равенств, процесс исключения переменных становится весьма трудоемкой процедурой. Кроме того, возможны ситуации, когда уравнения не удается разрешать относительно переменной. В частности, если в приведенном примере ограничения g(x)=0 задать в виде g(x)= ![]() +
+ ![]() +
+ ![]() , то получить аналитическое выражение какой-либо из переменных через другие не представляется возможным. Таким образом, при решении оптимизационных задач, содержащих сложные ограничения в виде равенств, целесообразно использовать метод множителей Лагранжа. С помощью этого метода находят необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничением в виде равенств. При этом задача с ограничением в виде равенств, преобразуется в эквивалентную задачу безусловной оптимизации.
, то получить аналитическое выражение какой-либо из переменных через другие не представляется возможным. Таким образом, при решении оптимизационных задач, содержащих сложные ограничения в виде равенств, целесообразно использовать метод множителей Лагранжа. С помощью этого метода находят необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничением в виде равенств. При этом задача с ограничением в виде равенств, преобразуется в эквивалентную задачу безусловной оптимизации.
Рассмотрим задачу, имеющую несколько ограничений в виде равенств:
минимизировать f(x) при ограничениях (x)=0, при j=1,2,....,k.
В соответствии с методом множителей эта задача преобразуется в следующую задачу безусловной оптимизации:
минимизировать L(x, )=f (x)- ![]()
![]()
![]() ,
,
где L(x, ![]() ) - функция Лагранжа,
) - функция Лагранжа, ![]() - множители Лагранжа.
- множители Лагранжа.
На знак ![]() никаких требований не накладывается.
никаких требований не накладывается.
Приравниваем частные производные L(x, ![]() ) по x к нулю, получаем следующую систему n уравнений с n неизвестными:
) по x к нулю, получаем следующую систему n уравнений с n неизвестными:
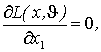 ...
...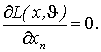 ,
,
Если найти решение приведенной выше системы в виде функций вектора оказывается затруднительным, то можно расширить систему путем включения в нее ограничений в виде равенств:
g1(x)=0,
g2(x)=0,
.........
gk(x)=0.
Решение расширенной системы, состоящей из n+k неизвестными, определяет стационарную точку функции L.
Пример № 1. Минимизировать ![]() при ограничении
при ограничении ![]() .
.
Соответствующая задача безусловной оптимизации записывается в следующем виде.
Минимизировать ![]()
Приравняв две компоненты градиента L к нулю, получим:
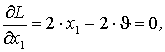
![]()
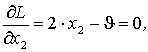
![]()
Поставив полученные значения ![]() в уравнение
в уравнение ![]() , получим,
, получим, ![]() т.е.
т.е. ![]() . Следовательно,
. Следовательно, ![]()
![]()