Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.5.1. Условия Куна–Таккера

Метод множителей Лагранжа можно использовать при построении критериев оптимальности для задач с ограничениями в виде равенств. Кун и Таккер обобщили этот подход на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств. Рассмотрим следующую общую задачу нелинейного программирования:

Минимизировать f(x) при ограничениях: ,

 ,

где .

Ограничения в виде неравенства  называется активным, или связывающим, в точке , если , и неактивным, или не связывающим, если  где - допустимая точка, то есть удовлетворяющая всем ограничениям. Если существует возможность обнаружить ограничения, которые неактивны в точке оптимума, до непосредственного решения задачи, то эти ограничения можно исключить из модели и тем самым уменьшить ее размеры.

Кун и Таккер построили необходимые и достаточные условия оптимальности для задач нелинейного программирования, исходя из предположения о дифференцируемости функций  Итак, задача Куна - Таккера состоит в том, чтобы найти векторы   удовлетворяющие следующим условиям:

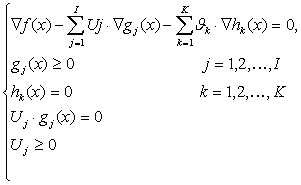
               (2-1)

Прежде всего, проиллюстрируем условия Куна-Таккера на примере.

Минимизировать  при ограничениях:

Записав данную задачу в виде задачи линейного программирования, можно получить:

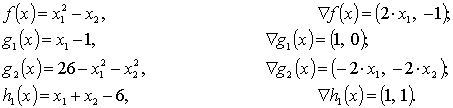
Уравнение (1), входящее в состав условий Куна-Таккера (система (2-1)), принимает следующий вид:

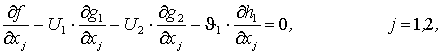
откуда 

Неравенства (2) и уравнения (3) задачи Куна-Таккера в данном случае записывается в виде:

Уравнения (4), известные как условие дополняющей нежесткости, принимают вид:

Заметим, что на переменные U₁ и U₂  накладывается требование неотрицательности, тогда как ограничение на знак , отсутствует. Таким образом, для данной задачи условия Куна-Таккера записываются в следующем виде: