Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.5.2. Необходимость условий Куна–Таккера

Теорема 1. Пусть f, g_j и h_k - дифференцируемые функции, а x^* - допустимое решение данной задачи. Далее пусть  и  линейно независимы. Если x^* - оптимальное решение задачи нелинейного программирования, то существует такая пара векторов  что  является решением задачи Куна-Таккера, то есть системы (2-1).

Проверка выполнения условия  линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свойствами.

• 1. Все ограничения в виде равенств и неравенств содержат линейные функции.
• 2. Все ограничения в виде неравенств содержат вогнутые функции, все ограничения - равенства - линейные функции, а также существует по крайней мере одна допустимая точка , которая расположена во внутренней части области, определяемой ограничениями- равенствами. Другими словами, существует такая точка , что:

Необходимые условия Куна-Таккера можно использовать для доказательства того, что заданная допустимая точка, удовлетворяющая условию линейной независимости, не является оптимальной, если она не удовлетворяет условиям Куна-Таккера. С другой стороны, если в этой точке и выполняются условия Куна-Таккера, то нет гарантии, что найдено оптимальное решение нелинейной задачи.

Рассмотрим пример.

    Минимизировать  при ограничении

    Запишем условия Куна-Таккера:

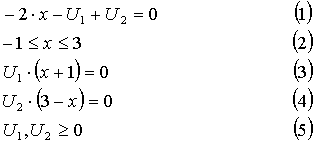                (2-2)

Так как ограничения содержат линейные функции, условие линейной независимости выполняется во всех допустимых точках. Легко видеть, что х = 3- точка оптимума. Рассмотрим допустимое решение х = 2. Для того, чтобы  доказать его неоптимальность, проверим выполнение условий Куна-Таккера. Из уравнений (3) и (4) системы (2-2) следует, что U₁=U₂=0; однако значения х=2, U₁=U₂=0 не удовлетворяют уравнению (1). Следовательно, исходя из необходимых условий   Куна- Таккера, точка х=2  не может быть оптимальной.

С другой стороны, решение х=U₁=U₂=0, то есть х- другая точка из допустимой области, удовлетворяет системе (1)-(5) и, следовательно, определяет точку  Куна-Таккера, однако оптимальным не является. Условия  Куна-Таккера должны выполняться в точке оптимума х=3. Нетрудно проверить, что решение х=3 и U₁=0, U₂=6 удовлетворяет условиям  Куна-Таккера.