Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.5.3. Достаточность условий Куна–Таккера

Теорема 2. Пусть целевая функция f(x) выпуклая, все ограничения в виде неравенств содержат вогнутые функции g_j(x),  j=1,2,...,I, а ограничения в виде равенств содержат линейные функции h_k(x), k=1,2,...K. Тогда если существует решение (x^*,U^*, ), удовлетворяющее условиям   Куна-Таккера, то x^* - оптимальное решение задачи нелинейного программирования.

Если условия теоремы 2 выполняются, то нахождение точки Куна-Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим следующий пример.

Минимизировать  f (x) = x₁² - x₂ ограничениях:

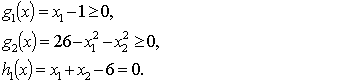
С помощью теоремы 2 докажем, что решение  является оптимальным. Для этого необходимо рассмотреть следующие понятия.

Функция n переменных f(x) называется выпуклой функцией тогда и только тогда, когда для любых двух точек x₁ и x₂ , принадлежащих множеству Д, и  0 ≤ λ ≤ 1 выполняется неравенство:

Матрица Гессе для функции f(x) есть симметричная матрица порядка n x n

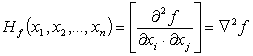
Функция f(x) выпуклая, если ее матрица Гессе положительно определена или положительно полу определена для всех значений  x₁, x₂, ...x_n, т.е. диагональные элементы должны быть >0. Функция f(x) выпуклая, если ее матрица Гессе отрицательно определена или отрицательно полуопределена для всех значений  x₁, x₂, ...x_n.

Для данной задачи имеем:

 и .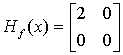

Так как матрица H_f(x) положительно определена при всех х, функция f(x) оказывается выпуклой. Первое ограничение в виде неравенства содержит линейную функцию g₁(x), которую можно считать вогнутой. Для того чтобы показать, что функция g₂(x) является  вогнутой, вычислим

 и .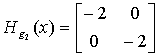

Поскольку матрица   отрицательно определена, функция g₂(x) является вогнутой. Функция h₁(x) входит в линейное ограничение в виде равенства. Следовательно, все условия теоремы 2 выполнены. Если показать, что x^* =(1;  5)- точка Куна - Таккера, то действительно установится оптимальность решения x^*.

Условия Куна - Таккера для данного примера имеют вид:

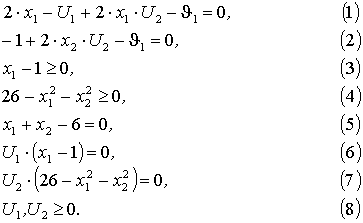                (2-3)

Точка x^* =(1;  5) удовлетворяет ограничениям (3)-(5) системы (2-3) и, следовательно, является допустимой. Уравнения (1) и (2)  принимают следующий вид:

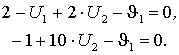
Положив , получим U₂=0,1 и  U₁=2,2. Таким образом, решение x^* =(1;  5), и U^* =(2.2 ,0.1) и  удовлетворяет условиям Куна-Таккера. Поскольку условия теоремы 2 выполнены, то  x^* =(1;  5) - оптимальное решение. Заметим, что существуют так же и другие значения U₁, U₂ и  , которые удовлетворяют системе (2-3).

Рассмотрим пример.

Требуется минимизировать

при ограничениях:

Составим уравнения, входящие в состав условий  Куна - Таккера.

• 1. Функция Лагранжа имеет вид:

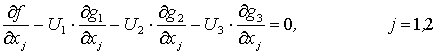
откуда:       .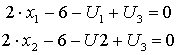

• 2. Условия дополняющей нежесткости:

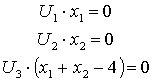
Следовательно, необходимо решить 5 уравнений с 5 неизвестными. 3 последних уравнения содержат произведение 2-х сомножителей, каждое из которых может быть равно 0, поэтому необходимо рассмотреть все возможные случаи (8 вариантов). В 3 главе рассмотрен ряд практических задач, демонстрация которых показывает, что уже при анализе возможных вариантов может быть получено оптимальное решение.