
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
2.6.1. Вариационное исчисление
В ряде задач для описания геометрических характеристик непрерывно изменяющихся поперечных сечений элемента конструкции механической системы требуется введение функций, задающих форму элемента. Для определения характерных свойств данного класса задач рассмотрим сначала два типичных примера.
|
Рис. 2.1. Пример 1.
|
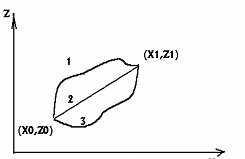
Пример 1.Требуется найти кратчайшую кривую между двумя точками (x0,z0) и (x1, z1) на плоскости X и Z. Любой кривой, соединяющей две заданные точки, сопоставляется ее длина. Задача состоит в том, чтобы выбрать кривую z(x), имеющую наименьшую длину. Для кривой z(x) длина определяется выражением: |
f(x)=∫ (1+(![]() )2)0,5dx.
)2)0,5dx.
Пример 2. В вертикальной плоскости заданы две точки (x0, z0) и (x1,z1), не лежащие на одной вертикальной прямой. Требуется найти соединяющую эти точки кривую, вдоль которой материальная точка, находившаяся в состоянии покоя в (x0,z0), будет скользить без трения в точку (x1,z1) за наименьшее время.
Пусть m - масса материальной точки, g - ускорение свободного падения. Так как тело начинает движение из состояния покоя (x0,z0), а трение отсутствует, то можно записать уравнение энергии в следующем виде:
![]() mV2=mg(z-z0),
mV2=mg(z-z0),
где V - скорость, определяемая по формуле:
V=((![]() )2+(
)2+( ![]() )2)0.5=(1+(
)2)0.5=(1+( ![]() )2)0.5
)2)0.5 ![]() ,
,
t- время движения материальной точки.
После преобразований представленных уравнений можно получить:
dt=(1+(![]() )2)0.5dx
)2)0.5dx![]() .
.
Следовательно, полное время t, необходимое для перемещения из (x0,z0) в (x1,z1), равно:
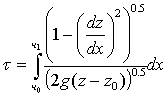 .
.
Данное выражение показывает, что t зависит от вида всей кривой, по которой скользит материальная точка. Такая задача сводится к нахождению кривой z(x), называемой брахистохроной.
Из приведенных примеров видно, что функция, описывающая кривую, должна определяться из решения оптимизационной задачи. Кроме того, значения минимизируемых величин определяется функциями, задающими указанные кривые. Поэтому рассматриваемые величины являются функциями от функций. Они называются функционалами. Типичным функционалом, встречающимся в вариационном исчислении, является интеграл.
Итак, оптимизационная задача ставится следующим образом: найти в классе функций, интегрируемых вместе с квадратом производных и удовлетворяющих граничным условиям, такую функцию z(x) при x0 x x1, которая минимизирует функционал f(x).
Приведенное обсуждение примеров 1 и 2 позволяет сформулировать основную задачу вариационного исчисления для более широкого класса задач. Найти дважды непрерывно дифференцируемую на интервале x0 x x1 функцию z(x), удовлетворяющую граничным условиям:
zi (x0)=zi0 для некоторых 1 i n,
zj(x1)=zj1 для некоторых 1 j n и минимизирующую функционал:
f(z)= 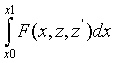 ,
,
где F - дважды непрерывно дифференцируемая по всем своим аргументам действительнозначная функция, а z'=[![]() ].
].
Указанные выше граничные условия означают, что кривые в примерах 1 и 2 проходят через заданные точки.
 x
x