Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.6.2. Частные случаи и примеры

В практических задачах вид функции  позволяет упростить дифференциальное уравнение второго порядка для функции z(x), необходимое для решения задачи вариационного исчисления. Такое уравнение называется уравнением Эйлера - Лагранжа и с использованием цепного правила дифференцирования сложной функции и обычных обозначений имеет вид:

.

Случай 1. F зависит только от z^', поэтому F=F(z^').

Для задачи из примера 1 необходимо найти кратчайшую кривую в плоскости x-z, проходящую через точки (0,  0) и (1,  1). При этом исследуемая функция имеет вид: F=(1+(z^')²)^1/2. Следовательно, уравнение Эйлера-Лагранжа записывается в виде:

(1+(z^')²)^-3/2z^"=0.

Так как (z^')² ≥ 0 , то z^"=0, поэтому: z=ax+b, где a и b - константы.

Отсюда следует, что кривая, кратчайшим образом соединяющая две заданные точки, является прямой линией, что и неудивительно. Из граничных условий следует: z(0)=b=0, z(1)=a=1. Поэтому решением данной задачи является функция: z(x)=x.

Случай 2. Пусть F зависит только от x и z^': F=F(x, z^'). В этом случае уравнение Эйлера - Лагранжа имеет вид:

,

поэтому: F_z'(x, z^')=c, где с - произвольная постоянная.

Случай 3. Функция z - вещественная, а F зависит только от z и z^':  F=F(z, z'). Уравнение Эйлера-Лагранжа в этом случае имеет вид:

F_z- F_z'z z'- F_z'z' z"=0.

Умножение на z' приводит к уравнению:

z' F_z-(z')²F_z'z- z'z"F_z'z'=0, что сводится к d(F-z'F_z')/dx=0. Следовательно, F-z' F_{z '}=C, где С - произвольная постоянная.

Решим задачу о брахистохроне (пример 2). Функция времени t равна находится из выражения:

,

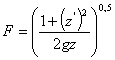где .

Уравнение из случая 3 записывается в виде:

.

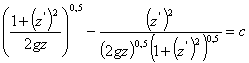Оно сводится к уравнению z(1+(z')²)=C₁, где С₁ - новая константа. Решение этого дифференциального уравнения представляет собой свойство циклоид, записанных в параметрическом виде:

x=C₂+C₁/2(S- sin S),  z=C₂/2(1- cos S).

Константы С₁ и С₂ выбираются путем выделения соответствующей циклоиды, проходящей через заданные точки.

Изложенный подход, который иногда применяется совместно с одним из численных методов, например, методом наискорейшего спуска, может явиться основой для создания вычислительных алгоритмов в решении статических и динамических задач проектирования элементов РК. К их можно отнести следующие.

• 1. Колонна наименьшего веса, способная выдержать, например, заданную сжимающую нагрузку. Поскольку поперечное сечение определяется только переменными, определяющими ее форму, то задача сводится к исследованию функционала, т.е. к решению уравнения Эйлера-Лагранжа. Подобный алгоритм применим для колонн с различными граничными условиями и формой поперечного сечения.
• 2. Упругие системы (балки, пластины и другие силовые конструкции) переменной толщины, рассчитываемые на изгиб, колебания и устойчивость при наличии ограничений на напряжения, перемещения, собственные частоты колебаний и размеры конструкций.
• 3. Балки и пластины, к которым приложены динамические нагрузки. Несмотря на идеализацию при постановке указанных задач, получаемое решение для простых конструкций обладает характерными особенностями, применимыми и для сложных элементов РК.