
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
2.7.1. Стандартная форма задач линейного программирования
Задачами линейного программирования называются оптимизационные задачи, в которых ограничения, представленные в виде равенств или неравенств, и целевая функция линейна. Разработка модели ЛП включает следующие основные этапы: определение переменных задачи, представление её ограничений в виде линейных уравнений или неравенств, задание линейной целевой функции, подлежащей минимизации или максимизации.
Задача ЛП в стандартной форме с m ограничениями и n переменными имеет следующий вид:
максимизировать или минимизировать ![]()
при ограничениях:
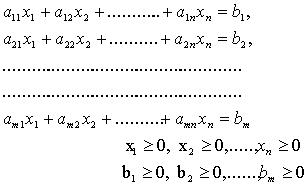 .
.
Задачи ЛП в стандартной форме можно записать в компактных матричных обозначениях следующим образом:
максимизировать или минимизировать ![]()
при ограничениях ![]()
где A - матрица размерности mxn, x - вектор-столбец размерности nxl, b- вектор-столбец размерности mxl, а c - вектор-строка размерности .1xn.
Обычно A назначается матрицей коэффициентов, x - вектором переменных, b - вектором ресурсов, c - вектором оценок задачи ЛП.
При решении задачи ЛП симплекс-методом требуется, чтобы задача была представлена в стандартной форме. Однако не все практические задачи ее имеют, поэтому для удовлетворения требования алгоритма необходимо следующее.
- 1. При помощи введения дополнительных остаточных или избыточных переменных преобразовать неравенства в равенства.
- 2. Для получения неотрицательных переменных задачи неограниченные по знаку переменные заменить разностью двух неотрицательных.
При решении задач ЛП используются следующие основные понятия. Допустимым решением являются неотрицательные значения переменных, для которых выполняются ограничения, а допустимой областью - совокупность допустимых решений. Оптимальным решением называются такие допустимые значения переменных, при которых ЦФ экстремальна, т.е. имеет оптимальное значение. В ряде случаев, ЦФ имеет одно оптимальное значение при нескольких комбинаций значений переменных, следовательно, задача обладает неединственностью оптимума. Когда в задаче ЛП нет конечного оптимума, то в этом случае существует неограниченный оптимум.