Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.7.2. Основы симплекс-метода

Рассмотрим задачу ЛП с  m ограничениями и  переменными, записанную в стандартной форме. Как правило, число уравнений задачи меньше числа переменных (т.е. m < n ), поэтому множество её допустимых решений бесконечно. Следовательно, выбор наилучшего допустимого решения, максимизирующего f (x), нетривиален.

Известен классический метод решения систем линейных уравнений, называемый методом Гаусса - Жордана. Основная идея этого метода состоит в сведении системы  m уравнений с n  неизвестными к каноническому или ступенчатому виду при помощи элементарных операций над строками. К ним относятся:

• 1. Умножение любого уравнения системы на положительное или отрицательное число.
• 2. Прибавление к любому уравнению другого уравнения системы, умноженного на положительное или отрицательное число.

При использовании первых  m переменных ( ) каноническая система имеет следующий вид:

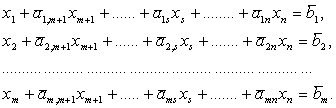                           (2-4)

Переменные  входящие с единичными коэффициентами только в одно уравнение системы и с нулевыми - в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствуют ровно одна базисная переменная. Остальные  n - m переменных ( ) называются независимыми или небазисными. При записи системы в каноническом виде все её решения можно получать, присваивая независимым переменным произвольные значения и решая затем получающуюся каноническую систему относительно зависимых переменных. Базисным решением системы в каноническом виде называется решение, полученное при нулевых значениях небазисных переменных.

Например, в системе (2-4) одно из базисных решений задаётся как  Если  к тому же неотрицательны, то полученное решение называется допустимым базисным решением. В указанной системе  для удобства записи в качестве базисных используются первые  m переменных. В действительности для получения канонической системы уравнений и базисного решения любые  m из n  переменных можно выбрать в качестве базисных.

Это означает, что максимальное число базисных решений задачи ЛП с  ограничениями и  переменными, записанной в стандартной форме, конечно и выражается следующим образом:

.

Интуитивный подход к решению задачи ЛП, обладающий оптимальным решением, состоит в нахождении при помощи метода Гаусса - Жордана всех возможных допустимых базисных решений и последующем выборе решения, которому соответствует наилучшее значение целевой функции. Однако при решении задач ЛП симплекс-методом оказывается более эффективным, так как при этом анализируется лишь часть всех допустимых базисных решений.

Симплекс-метод разработан Дж. Данцигом. Он представляет собой итерационную процедуру решения задач ЛП, записанных в стандартной форме. При этом требуется, чтобы система ограничений - равенств была приведена к каноническому виду, что даёт возможность легко находить допустимое базисное решение. Алгоритм симплекс-метода включает следующие основные шаги.

• 1. Выбор начального допустимого базисного решения.
• 2. Переход от начального решения к другому допустимому базисному решению с лучшим значением целевой функции. На этом шаге исключаются из рассмотрения все допустимые базисные решения, которые хуже текущего решения. В силу этого обстоятельства симплекс-метод гораздо эффективнее упомянутого выше "прямого" подхода к решению задач ЛП.
• 3. Продолжение поиска допустимых базисных решений, улучшающих значения целевой функции. Если некоторое допустимое базисное решение нельзя улучшить, оно является оптимальным, и алгоритм симплекс-метода завершает свою работу.

Рассмотрим шаг 2 симплекс-метода в предположении, что базисное решение, задаваемое системой (2-4), допустимо. Пусть допустимое базисное решение задано в следующем виде:

базисные переменные

небазисные переменные

Множество базисных переменных называется базисом и обозначается через x_B. Вектор коэффициентов при базисных переменных обозначается через c_B. Для начального базиса:

Поскольку небазисные переменные равны 0, значение целевой функции f(x), соответствующее начальному допустимому базисному решению, находится по формуле:

.

Симплекс-метод даёт возможность проверить существование допустимого базисного решения с большим значением f(x). Для этого сначала проводится проверка оптимальности рассматриваемого решения. Если оно не оптимально, симплекс-метод позволяет перейти к смежному допустимому базисному решению с большим (или, по крайней мере, не меньшим) значением f(x). Оно отличается от рассматриваемого только одной базисной переменной.

Для получения смежного допустимого базисного решения симплекс-метод превращает одну из базисных переменных в небазисную и вводит одну из небазисных переменных в базис. Их необходимо выбрать так, чтобы замена одной из них на другую давала максимальное приращение целевой функции. В любом допустимом базисном решении базисные переменные положительны, а небазисные равны 0. Следовательно, превращение небазисной переменной в базисную приводит к увеличению её значения от 0 до некоторой положительной величины. Вводимая в базис переменная должна давать улучшение значения f(x). Для выбора вводимой в базис переменной следует присвоить небазисной переменной значение, равное 1, и вычислить изменение целевой функции.

Рассмотрим небазисную переменную . Пусть ей присвоено значение, равное единице; исследуем получаемое при этом изменение целевой функции. При этом следует учесть, что, поскольку рассматриваются только смежные допустимые базисные решения, то остальные небазисные переменные по прежнему равны нулю, поэтому систему (2-4) можно переписать в следующем виде:

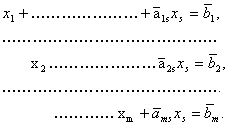           (2-5)

Из системы (2-5) при  возрастании  от 0 до 1 получаем новое решение:

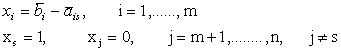
Новое значение целевой функции находится по формуле:

Обозначим через приращение величины f(x), получающееся при увеличении значения  на единицу. Таким образом, величина  определяется из выражения:

.

Величина   называется относительной оценкой небазисной переменной , тогда как c_S является исходной оценкой x _s  целевой функции. Если c_s >0, то можно добиться увеличения целевой функции f(x), вводя переменную  x в базис. Уравнение, определяющее относительную оценку, называется правилом скалярного произведения. Относительная оценка небазисной переменной x_j обозначается через  и определяется по формуле:

где c_B соответствует оценкам базисных переменных, а  представляет собой  j-й столбец в канонической системе, соответствующей рассматриваемому базисному решению.

Если относительные оценки небазисных переменных допустимого базисного решения задачи максимизации отрицательны или равны 0, то решение оптимально. Ясно, что если для всех небазисных переменных, то любому смежному допустимому базисному решению соответствует значение целевой функции, не превосходящее уже достигнутое. Отсюда следует, что в рассматриваемой точке имеется максимум. Поскольку целевая функция f(x) линейна, он совпадает с глобальным. Для пояснения предположим, что  и, следовательно, начальное допустимое базисное решение нежелательно. Поскольку величина  положительна, при увеличении значения небазисной переменной  на единицу f(x) возрастает на . Чем больше увеличение значения x_s, тем больше приращение величины f(x), поэтому необходимо, чтобы значение  x_s было возможно большим. С другой стороны, при увеличении  значения остальных базисных переменных также меняются, и их новые значения находятся из системы (2-5):

.

Если  то x_i возрастает вместе с x_i ,а a_is = 0 при  значение x не меняется. Однако, если  переменная  x убывает с ростом  x_s и становится отрицательной при неограниченном увеличении x_s , а решение - недопустимым. Таким образом, максимально допустимое значение  x_s определяется следующим правилом:

.

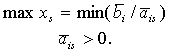Пусть .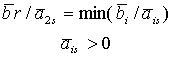

Следовательно, при увеличении  x_s до  базисная переменная  x₂ первой среди базисных переменных обращается в 0 и заменяется в базисе переменной x₂. Переменная x₂ становится новой базисной переменной в строке r-й, причём новое допустимое базисное решение имеет вид:

Поскольку при увеличении x_s на единицу приращение  f(x)составляет , для нового решения общее приращение f(x) определяется по формуле:

Уравнение, на основании которого определяются базисные переменные, выводимые из базиса, носит название минимального отношения. При использовании симплекс-метода вычисление относительных оценок всех небазисных переменных текущего допустимого базисного решения и проверка его оптимальности проводятся до тех пор, пока не будут выполнены условия оптимальности.

Пример. Использовать симплекс-метод для решения следующей задачи:

максимизировать ;

при ограничениях: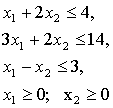

Приведение задачи к стандартной форме при помощи дополнительных переменных преобразует математическую модель к следующему виду:

максимизировать ;

при ограничениях: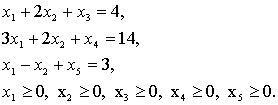

В допустимом базисном решении системы уравнений в каноническом виде базисными переменными являются  и . Последовательные итерации симплекс-метода удобно представлять в компактном виде, используя таблицу для записи ограничений и целевой функции. При этом проводятся вспомогательные вычисления, например, с использованием правила скалярного произведения, правила минимального отношения и элементарных преобразований.

Элементы таблиц представляют собой коэффициенты задачи (в табл.1 содержится начальное допустимое базисное решение). Заметим, что для каждого ограничения записаны лишь коэффициенты при входящих в него переменных. Коэффициенты целевой функции c_j  находятся  над коэффициентами соответствующих им переменных x_j. Понятие базис обозначает совокупность базисных переменных начальной таблицы (  x₃ для  ограничения 1, x₄ для ограничения 2, x₅ для ограничения 3), а символом c_B обозначается совокупность оценок переменных  c_j базиса. Из табл.1 находится начальное допустимое базисное решение:

Значение целевой функции f(x) задаётся скалярным произведением вектора  и вектора правых частей уравнений:

.

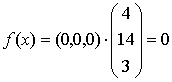Табл. 1.

Для проверки оптимальности найденного допустимого базисного решения следует вычислять относительные оценки переменных (пользуясь правилом   скалярного   произведения). Заметим, что относительные оценки  будут нулевыми, поскольку соответствующие переменные - базисные. Небазисные переменные  x₁ и x₂ имеют положительные относительно оценки. Следовательно, рассматриваемое допустимое базисное решение неоптимально. Небазисная переменная x₁ имеет наибольшую относительную оценку, поэтому её следует ввести в базис. Для определения переменной, выводимой из базиса, применяется правило минимального отношения. Вычисляются соотношения для всех ограничений с положительным коэффициентом при x₁:

Следует отметить, что для первой строки это отношение не вычисляется (оно принимается равным ∞), поскольку коэффициент при x₁, в строке 1 отрицателен. Это означает, что можно неограниченно увеличивать x₁, причём при этом значении  x₃ остаётся положительным. С другой стороны, из значения   для отношения во второй строке следует, что x₄ станет равным 0 при возрастании  x₁ до . Аналогично, если x₁  возрастает до 3, то x₅ обращается в нуль. Минимальное отношение равно 3, поэтому при возрастании  x₁ от 0 до 3 первой среди базисных переменной обратиться в 0 x₅ ; она заменится в базисе переменной x₁ . Третья строка называется ведущей строкой, а коэффициент при  в ведущей строке называется ведущим элементом. Элементарное преобразование приводит к системе с новыми базисными переменными x₃ , x₄ и x₁:

• 1) прибавить ведущую строку (строку 3) к первой, чтобы исключить переменную x₁ ;
• 2) умножить ведущую строку на (-3) и прибавить её ко второй строке, чтобы исключить x₁ .

Табл. 2

Для проверки оптимальности полученного в табл. 2 допустимого базисного решения необходимо вычислить вектор относительных оценок (строку ). Это можно выполнить, пользуясь правилом скалярного произведения. С другой стороны, новую строку  можно вычислить, применяя элементарное преобразование. Относительная оценка переменной x₁ должна быть равна 0, поскольку x₁ вошла в базис. Равенства нулю можно добиться, умножая третью строку на (-3) и прибавляя её к строке  . В результате автоматически получается новая строка  табл. 2.

Строка  табл. 2 всё ещё содержит положительный элемент, что указывает на возможность введения в базис небазисной переменной , улучшающей значение целевой функции. Применяя правило минимального отношения, находим из набора ( ). Переменная  должна занять место базисной переменной .

В табл. 3 представлено следующее допустимое базисное решение, полученное после выполнения элементарной операции. Поскольку в табл. 3 все элементы  строки  неположительные, она оптимальна. Оптимальное решение имеет следующий вид:  а оптимальное значение f(x)=14 .

Табл. 3

Представленный алгоритм метода ЛП, нашедший широкое применение для решения организационно - экономических задач, стал применяться и при проектировании элементов РК, например, при компоновке оборудования на ракете.