Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Автоматизированное проектирование технических систем: Учебное пособие.
Бельков В. Н., Ланшаков В. Л.,
2.8.1. Основные понятия и расчетные формулы
Отсутствие универсального метода решения общей задачи нелинейного программирования послужило причиной появления множества узкоспециализированных методов, приспособленных к решению отдельных задач. К таким методам относится и метод геометрического программирования, возникший и получивший развитие в связи с задачами инженерного проектирования.
Основное требование метода геометрического программирования состоит в том, чтобы и целевая функция, и ограничения были выражены в виде так называемых позиномов, имеющих вид:
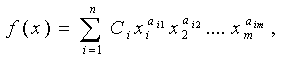(2-6)
где 
- произвольные вещественные числа.
Анализ известных формул расчета деталей машин, а также всевозможных условий прочности, жесткости, устойчивости и др., показывает, что большая часть из них выражается зависимостями вида (2-6). Именно это обстоятельство позволяет считать метод геометрического программирования удачным для решения задач оптимального проектирования объектов машиностроения.
По сравнению с другими методами оптимизации геометрическое программирование имеет следующие преимущества:
- позволяет выявить достаточно полную картину сравнительной значимости проекта и отдельных слагаемых частей целевой функции;
- минимальное значение целевой функции находится до определения оптимальных значений параметров;
- исходная задача с нелинейными целевой функцией и ограничениями сводится к двойственной задаче с нелинейной целевой функцией, но линейными ограничениями, решить которую легче, чем исходную задачу;
- имеется возможность количественной оценки степени трудности решаемой задачи;
- для реализации метода с применением ЭВМ можно разработать универсальный программный комплекс.
В общем случае исходную задачу геометрического программирования формулируют следующим образом - найти минимальное значение целевой функции f(x) при ограничениях 
, причем f(x) и левые части ограничений являются позиномами (2-6).
Одна из важнейших характеристик - степень трудности решаемой исходной задачи геометрического программирования определяют из выражения:
d = n-(m+1),
где n- общее число слагаемых членов во всех позиномах (целевой функции и ограничениях); т-число оптимизируемых параметров.
Степень трудности решаемой задачи характеризуется:
- - при d = 0 - сложностью решения системы n линейных уравнений;
- - при d = 1 - сложностью решения одного нелинейного и системы n линейных уравнений;
- - при d> 0 - сложностью решения системы d нелинейных алгебраических уравнений и n линейных уравнений.
Подход к оптимизации позиномиальных функций основан на неравенстве между средним арифметическим и средним геометрическим, согласно которому среднее геометрическое не превосходит среднего арифметического. Использование неравенства для средних привело к появлению термина геометрического программирования.
Проиллюстрируем метод геометрического программирования (ГП) в случае линейных ограничений
Неравенство для средних позволяет заключить, что для произвольных положительных чисел 
и таких чисел 
, что 
имеет место соотношение
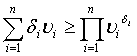, (2-7)
причем равенство достигается в случае 
. Полагая 
, можно переписать выражение (2-7) для любых величин 
и ,
, 
.
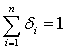
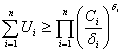Неравенство обращается в равенство только тогда, когда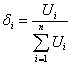 
. Пусть 
. Тогда ЦФ f(x) = 
.
Следовательно,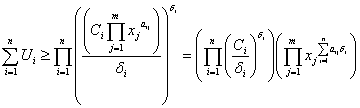 
.
Неравенство имеет место при любых 
, таких, что 
. Предположим, что имеет место соотношение: 
. Тогда неравенство сводится к системе соотношений: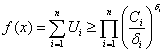 
для всех при 
и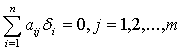 
.
Поскольку неравенство может обращаться в равенство, можно получить: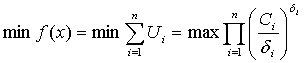 
,где δi удовлетворяет указанным соотношениям.
Рассмотрим следующую прямую задачу геометрического программирования.
Минимизировать 
при ограничениях 
. Двойственная задача имеет следующий вид.
максимизировать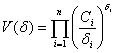 
при ограничениях:
1. 
, система неравенств называется условием неотрицательности;
2. 
, данное уравнение называется условием нормализации; следует учесть в дальнейшем, что оно составляется только для позиномов, входящих в ЦФ;
3. 
, указанная система уравнений называется условием ортогональности и составляется для всех позиномов; причем коэффициенты 
- вещественные числа, элементы матрицы экспонент (или показателей) исходной задачи.
Используя полученные выше неравенства и формулы, можно получить следующие соотношения между прямой и двойственной задачами. Наличие оптимального решения в двойственной задаче представляет собой достаточное условие существования оптимума в прямой задаче.
Для соответствующих оптимумов:
.
Прямое и двойственное оптимальные решения связаны соотношением:
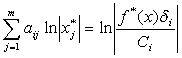или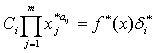 
.
Допустимое решение двойственной задачи дает нижнюю границу оптимального значения ЦФ. В случае ограничений, представленных позиномами, задача усложняется, однако подход остается аналогичным.