Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.8.2. Общий случай задачи ГП

Для вывода расчетной формулы воспользуемся основным тождеством:

.

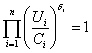Оно выполняется, так как по определению:

.

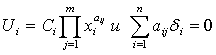Следовательно, .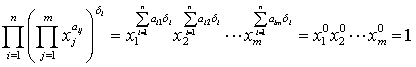

Рассмотрим k-е ограничение, содержащее, например, два позинома, записанных в общем виде: . Из соотношения пропорциональности: , можно получить: .

Введя обозначения позиномов  - для ЦФ и  - для ограничений, а также учитывая, что , из основного тождества получим:

,

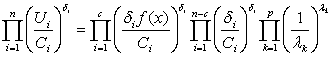где n - общее количество позиномов;

c - количество позиномов в целевой функции;

p - количество позиномов в k - м ограничении;

 - сумма двойственных переменных в k - м ограничении, она составляется отдельно для каждого ограничения.

Следовательно, .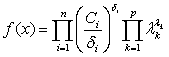

Задача 1. Пусть требуется минимизировать позином:

 

при ограничениях

.         

Заметим, что в задаче четыре члена и только три переменных. Двойственная функция этой задачи имеет вид:

.

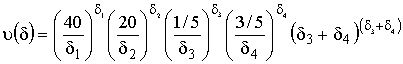Условие нормализации представляется уравнением:

а условия ортогональности-системой:

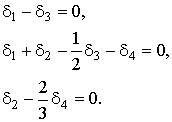
Эти условия образуют систему, состоящую из четырех линейных уравнений с четырьмя неизвестными, и имеют единственное решение ( ):

Значение двойственной функции в точке δ* таково:

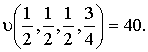
Так как δ* является единственной точкой области определения υ(δ), из теоремы двойственности мы заключаем, что минимум функции

Следует обратить внимание на то, что условный минимум функции f(x) был определен до нахождения минимизирующего вектора ( ). Исходя из смысла двойственной переменной, как весового коэффициента позинома, можно записать для ЦФ:  

 и         ,

а для ограничений:  и .

Чтобы определить значения , прологарифмируем обе части соотношений представленных выше соотношений. Мы получим, что , удовлетворяет системе:

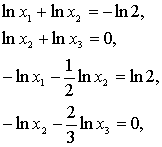
которая линейна относительно переменных lnx₁, lnx₂ и lnx₃. Она имеет единственное решение (-ln2, 0, 0), а это означает, что f(x) достигает условного минимума в точке (1/2, 1, 1).

Следовательно, поиск оптимизируемых параметров осуществляется путем решения системы уравнений, составленной из позиномов, число которых превышает количества неизвестных, однако любая комбинация уравнений дает одинаковый результат. Зачастую, для получения аналитических формул есть возможность преобразования расчетной системы уравнений без вычисления двойственной функции.

Если степень трудности равна нулю, то максимизирующий вектор δ* не зависит от коэффициентов позинома. Требование ортогональности, например, трехкомпонентного вектора δ двум вектор - столбцам матрицы показателей полностью определяет вектор на некотором двумерном подпространстве трехмерного пространства. Поэтому условие ортогональности может быть сформулировано следующим образом: вектор решения  должен быть ортогонален пространству показателей. Любой нормализованный вектор, ортогональный пространству показателей, называется двойственным вектором. Для его построения используется метод Бранда, который может быть использован к любой матрице показателей.

В соответствии с этим методом пространство, натянутое, например, на два вектор - столбца, остается неизменным при умножении любого из столбцов на постоянное число, а также при замене любого столбца на линейную комбинацию двух исходных столбцов. При использовании метода Бранда столбцы умножаются на константы, а затем берутся линейные комбинации таким образом, чтобы получилась единичная матрица в двух верхних строках матрицы показателей.

В предыдущей задаче размерность вектора показателей п была ровно на единицу больше размерности пространства показателей т, в результате чего условие ортогональности однозначно определяло двойственный вектор без проведения операции нормализации. Однако в общем случае n > т + 1,и поэтому условие ортогональности определяет лишь двойственное пространство. Размерность этого пространства равна n - m. Очевидно, что произвольный n-мерный вектор v может быть записан как v=e+δ,

где е-вектор показателей, а δ - двойственный вектор.

С целью записи общего выражения для вектора δ, лежащего на гиперплоскости нормализации, вводится понятие вектора невязки. Вектор невязки δ^(s) определяется как вектор, удовлетворяющий условию нормализации вида:

.

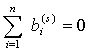Затем выбирается произвольный вектор δ, удовлетворяющий данному условию, например b⁽⁰⁾. Тогда общее выражение для вектора δ, лежащего на гиперплоскости нормализации, будет иметь вид:

.

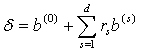Рис. 2.3. Графическая иллюстрация вектора нормализации и невязки.

Здесь d на единицу меньше размерности двойственного подпространства, а именно d=n-(m+1). Ранее величина d была названа степенью трудности задачи. Коэффициенты rs, общее число которых равно d, называются базисными переменными. Понятия векторов нормализации и невязки могут быть проиллюстрированы в двумерном случае. На рис. 2.3 гиперплоскость нормализации представляет собой прямую.

Любой вектор, идущий от начала координат с концом, лежащим на этой прямой, может быть выбран в качестве вектора нормализации. Любой вектор, лежащий на прямой нормализации, может быть выбран в качестве вектора невязки.Для демонстрации использования векторов нормализации и невязки рассмотрим задачу минимизации выражения:

 при условии .

Ниже для рассматриваемой задачи приведена матрица для пространства показателей и ее двойственное пространство:

  .

Последние два вектора двойственного пространства получены методом Бранда. Оба они удовлетворяют условию нормализации, поэтому любой из них может быть выбран в качестве вектора нормализации. Двойственный вектор невязки может быть получен просто как разность между этими двумя векторами, каждый из которых удовлетворяет представленному выше условию. Тогда формула:

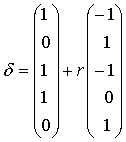
представляет собой наиболее общее выражение для двойственного вектора, удовлетворяющего условию нормализации.

Задача 2. Пусть нужно минимизировать позином:

       

при                                                                             

Соответствующая этой задаче двойственная задача состоит в максимизации двойственной функции:

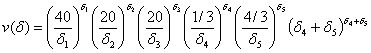
при двойственных ограничениях:

δ₁≥0, δ₂≥0, δ₃≥0, δ₄≥0, δ₅≥0,       - условие неотрицательности,       

δ₁ + δ₂ + δ₃ = 1                           - условие нормализации,

-δ₁ + δ₂ + δ₃ - 2δ₄ = 0,

-1/2δ₁ + δ₃ - 2δ₄ + 1/2δ₅ = 0,       - условия ортогональности,          

-δ₁ + δ₂ + δ₃ - δ₅ = 0.

Базисные векторы двойственного пространства получаются при использовании стандартной процедуры линейной алгебры, что является в данном случае методом Бранда. На первом шаге при помощи элементарных операций над столбцами матрицы экспонент она приводится к матрице «диагонального типа»:

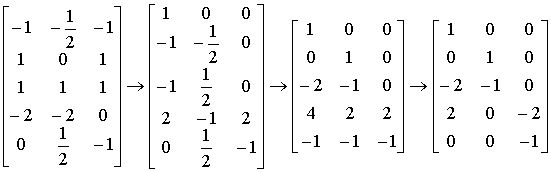   (2-8)

Результирующая матрица «диагонального типа» может быть записана в более удобной форме:

,                                                                                    (2-9)

в которой третью и пятую строки матрицы (2-8) необходимо было поменять местами, чтобы получить единичную (3 x 3) - матрицу в верхней части матрицы. Далее, берут с обратным знаком матрицу, транспонированную к матрице, лежащей ниже единичной (3 x 3)-матрицы, и дописывают к ней снизу единичную (2 x 2)-матрицу; в результате получается:

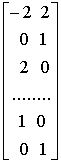.                                                                                             (2-10)

Из построения ясно, что любой вектор-столбец этой матрицы ортогонален ко всем вектор - столбцам матрицы (2-9). Однако нумерация компонент этих вектор - столбцов не соответствует нумерации в матрице (2-8), так как при переходе от (2-8) к (2-9) третья и пятая строки поменялись местами. Поэтому, меняя местами третью и пятую строки матриц (2-9) и (2-10), получают соответственно следующие матрицы:

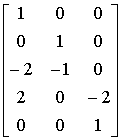        (2-11)         и  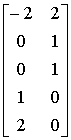               .             (2-12)

Вектор - столбцы матрицы (2-12) по построению ортогональны к вектор - столбцам матрицы (2-11). Так как матрицы (2-11) и (2-8) одинаковы, а (2-8) получена из матрицы экспонент при помощи элементарных операций над столбцами, можно заключить, что вектор - столбцы матрицы (2-12) ортогональны вектор - столбцам матрицы экспонент. Кроме того, вектор - столбцы матрицы (2-12) линейно независимы, они образуют базис пространства решений условий ортогональности. Разделив первый вектор-столбец матрицы (2-12) на сумму первых трех его компонент, можно получить вектор:

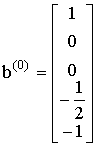,                                                                              (2-13)

который удовлетворяет как условию ортогональности, так и условию нормализации. Таким образом, b⁽⁰⁾ является вектором нормализации для задачи 2.

Так как матрица (2-12) имеет только два столбца, то для задачи существует лишь один вектор невязки b⁽¹⁾. Чтобы получить его, необходимо вычесть из оставшегося вектор - столбца матрицы (2-12) произведение суммы первых трех его компонент на вектор нормализации b⁽⁰⁾. В результате получается вектор:

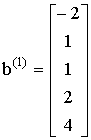.                                                                               (2-14)

Общее решение условий нормализации и ортогональности имеет вид

, или

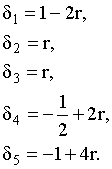                                                                            (2-15)

Важно отметить, что вторым способом нахождения векторов нормализации и невязки является метод подстановки, заключающийся в обозначении одних двойственных переменных через базисные, число которых, как уже отмечалось, определяется степенью трудности решаемой задачи, и выражении других переменных из представленных выше условий. В данном случае при  получается аналогичный результат. Из полученных уравнений ясно, что δ удовлетворяет условиям неотрицательности только при таких значениях r:

 .                                                                                 (2-16)

Подставляя в соотношения (14) значения r, равные, например, 1/4, 3/10 и 7/20, и вычисляя соответствующие значения двойственной функции, можно получить:

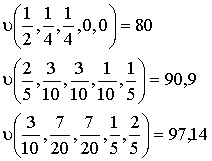                                                       (2-17)

Вычисляя f(x) для пробных значений x₁, x₂, x₃, которые удовлетворяют ограничениям прямой программы, получится:

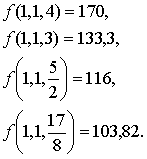                                                                    (2-18)

Из соотношения двойственности можно записать:

,

где x* - минимизирующий вектор задачи 2, a x и δ - произвольные векторы, удовлетворяющие соответственно ограничениям прямой задачи и двойственным ограничениям. Следовательно, (2-17) дает оценки снизу для значения f(x*), тогда как (2-18) дает оценки сверху. В частности,

.

Следовательно, можно считать, что условный минимум ЦФ равен 100 с погрешностью, не превышающей 4%.