Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

2.8.3. Решение задач ГП с ненулевой степенью трудности

Для получения однозначного решения необходимо рассмотреть би-двойственную функцию:

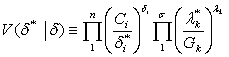,                                                   (2-19)

которая обладает замечательным свойством, состоящим в том, что она не зависит от направления нормализованного вектора δ в двойственном пространстве. В дальнейшем это свойство используется для получения единственного направления вектора δ*. При этом решение  должно быть заменено выражением вида:

.

Последнее соотношение не зависит от двойственного вектора δ, поскольку последний лежит на гиперплоскости нормализации. Пусть δ' и δ" - два каких-либо двойственных вектора. Поэтому можно записать следующие выражения:

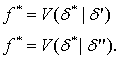
Разделив первое уравнение на второе, получим:

1 = (δ* | δ'''),

где δ''' = δ' - δ''.

Так как векторы δ' и δ" лежат на гиперплоскости нормализации, их разность δ"' представляет собой вектор невязки. Учитывая, что имеется d независимых векторов невязки, получаем следующие d независимых уравнений:

1 = V(δ^* | b^(s)), s = l,...,d.                                                          (2-20)

Теперь V* содержит d неизвестных, а именно d базисных переменных r_s:

,

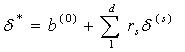поэтому уравнений (2-20) достаточно для того, чтобы полностью определить базисные переменные.

При решении практических задач в формуле (2-20) удобно разделить известные постоянные и неизвестные базисные переменные. С этой целью, используя формулу (2-19), перепишем соотношение (2-20) в виде:

.

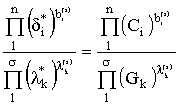Эти уравнения имеют такой же вид, что и уравнения равновесия в химии, поэтому называются уравнениями равновесия. Например, для задачи, представленной в разд. 2.7.2, можно записать:

,

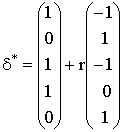что дает единственное уравнение равновесия:

.

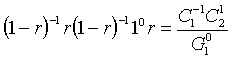После преобразований можно записать:

.

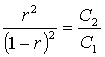Данное уравнение равновесия может быть непосредственно решено относительно r:

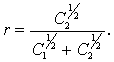
Если целевая функция является более сложной, например:

то соответствующее уравнение равновесия имеет вид

,

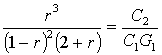которое необходимо решить численно.

Следовательно, метод ГП можно отнести к классу аналитических при нулевой степени трудности, а при d > 0 необходимо решать одно или несколько нелинейных уравнений, что является относительно простой задачей при современном уровне вычислительной техники, поэтому ГП должно найти широкое применение при проектировании элементов и агрегатов, а также РК в целом.