Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Автоматизированное проектирование технических систем: Учебное пособие.

Бельков В. Н., Ланшаков В. Л.,

3.1.2. Цилиндрическая пружина, работающая на кручение

Указанная формула содержит следующие параметры: N - число активных витков; Q - число неактивных витков; D - средний диаметр спирали; d - диаметр проволоки; р - плотность материала пружины ; g- ускорение свободного падения.

Соотношение между моментом и углом закрутки имеет вид:

где Θ - измеряется в градусах; Е - модуль Юнга.

Следовательно,

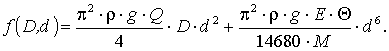
Напряжение изгиба в проволоке определяют по формуле:

где К₁ - коэффициент концентрации напряжений;

.

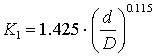Задача заключается в том, что используя условие Куна - Таккера, необходимо определить оптимальные параметры пружины при ограничениях на напряжения и знак величин d и D.

Функция Лагранжа имеет вид:

L = f(x)+ng(x),

где ЦФ определяется по формуле:

f(x)=0.25p ²ρgQDd d²+π d²QρgEqd⁶ /(14680 М),

ограничения в данном случае: g(x)=14.5 М /(D^0.115·d^2.885)-σmax.

Расчетная система уравнений имеет вид:

¶ L/¶ d=6π²ρgEq d⁵ /(14680m)+p²ρgDd/2-2.885·14.5 Мν/(D^0.115·d^3.885)=0;            (1)

¶ L/¶ D=π²Qρgd²/4-0.115·14.5Мν/(D^1.115·d^2.885)=0.                                              (2)

Анализ показывает, что, если ν=0, то из уравнения (2) d=0, что противоречит постановке задачи. Следовательно , g(x)=0, поэтому:

14.5М/(D^0.115·d^2.885)= σmax                                                                                      (3)

Итак, получена система трех уравнений (1),(2) и (3) с тремя неизвестными D,d и ν. Для ее решения сначала умножим уравнение (1) на 0.115d, а (2) уравнение - на (-2.885D) и сложим их, тем самым исключив ν. Из полученного уравнения

0.69 π²QρgEqd⁶/14680 - 2.655p²ρgQDdІ/4=0

выразим D: D=7.081·10^-5 Eqd⁴/(μQ)                         

полученное выражение подставим в (3):

0.3332(Eq/ μQ)^0.115·d^3.345=14.5μ/ σmax.                                                             (4)

Окончательно получим:

d=( μQ/ Eq)^0.03438·(43.517μ/ σmax)^0.299.

Внешний диаметр пружины D можно выразить из формулы (4):

D=7.9·10^-3(Eq/ μQ)^0.8625·(μ/ σmax)^1.196

Следовательно, совместное применение формул по курсу «Детали машин» и метода оптимизации позволило получить аналитические выражения для параметров пружины, минимизируюших ее вес.